Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Interferência de Ondas Sonoras

Ver Teoria
Exercício 321234567891011121314151617181920212223242526272829303133343536

Enunciado

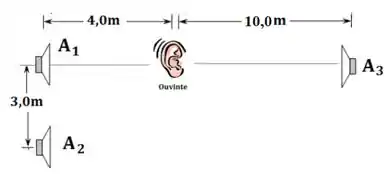
Três alto-falantes A 1 ,   A 2 e A 3 emitem ondas sonoras idênticas e em fase. Os alto-falantes estão em posições diferentes em relação ao ouvinte, mas todos estão contidos em um mesmo plano, como ilustrado na figura. Considere toda faixa de audição de um ser humano médio, 20 H z   a   20   K H z , e velocidade do som no ar igual a 340   m / s .

  1. Suponha que o alto-falante A 3 está desligado, ou seja, considere apenas os alto-falantes A 1   e   A 2 . Nesse caso, quais são os comprimentos de onda que fazem com que nenhum sinal sonoro seja detectado pelo ouvinte?
  2. Ainda nesse caso, quantas possíveis frequências existem na faixa de audição do ser humano médio?
  3. Agora, suponha que o alto-falante A 3 foi ligado, de forma que os três alto-falantes estão emitindo ondas sonoras. Nesse caso, qual é a menor frequência que faz com que o som que chegue ao ouvinte tenha a maior amplitude possível?

Passo 1

Para que a intensidade do som seja mínima, a interferência das ondas advindas de A1 e A2 é destrutiva. A diferença entre os caminhos percorridos pelas ondas emitidas pelos alto-falantes A1 e A2 deve ser um múltiplo semi-inteiro do comprimento de onda ( λ ). A distância entre A1 e o ouvinte é L 1   = 4 m e a distância entre A2 e o ouvinte é L 2 = 4 2 + 3 2 = 5 m . Portanto, para haver interferência destrutiva devemos ter:

λ = ∆ L 21 n + 1 2 = ( L 2 - L 1 ) / ( n + 1 2 ) = ( 5 - 4 ) / ( n + 1 2 ) = 1 / ( n + 1 2 ) , onde n = 0,1 , 2 …

Passo 2

Para encontrar o número n de possíveis frequências na faixa que um humano médio pode escutar, faz-se f m a x   = 20   K H z :

f m á x = 20000 H z = 340 n + 1 2 H z

n ≅ 58

Mas como nosso n começa de zero, estaremos no 59 ° harmônico.

Passo 3

Para que a amplitude seja máxima, a interferência das ondas sonoras emitidas pelos alto-falantes deve ser construtiva. Para que que isso aconteça a diferença entre os caminhos percorridos pelas ondas deve ser um múltiplo inteiro do comprimento de onda, de modo que:

λ = ∆ L n

Como são três alto-falantes, temos:

λ = ∆ L 21 n 1 = ( L 2 - L 1 ) / n 1 = 5 - 4 / n 1 = 1 / n 1 metros, com n 1 = 1,2 , 3 . .

λ = ∆ L 32 n 2 = ( L 3 - L 2 ) / n 2 = 10 - 5 / n 2 = 5 / n 2 metros, com n 2 = 1,2 , 3 …

λ = ∆ L 31 n 3 = ( L 3 - L 1 ) / n 3 = 10 - 4 / n 3 = 6 / n 3 metros, com n 3 = 1,2 , 3 …

Devemos considerar apenas os comprimentos de onda que permitem que as três interferências sejam construtivas simultaneamente, o que ocorre quando n 2 =   5 n 1   e   n 3 = 6 n 1 , ou seja, a amplitude é máxima quando:

λ = 1 / n 1   metros, com n 1 = 1,2 , 3 . .

Portanto, o maior comprimento de onda (que dará origem à menor frequência é λ = 1 m , que ocorre quando n 1   =   1 .   Como a v s o m = λ f , segue que:

f = v λ = 340 1 = 340 H z

Resposta

A)     λ = 1 / ( n + 1 2 )

B)     n ≅ 58 ,   59 ° harmônico.

C) 340 H z

Exercícios de Livros Relacionados

A figura mostra duas fontes pontuais F 1 e F 2 que emitem sons de comprimento de onda λ = 2,00m . As emissões são isotrópicas e em fase; a distância entre as fontes é d = 16,0m . Em qualquer ponto P s
Uma onda sonora senoidal se propaga no ar, no sentido positivo de um eixo x , com uma velocidade de 343 m / s . Em um certo instante, a molécula A do ar está em seu deslocamento máximo no sentido nega
Na figura abaixo temos as ondas sonoras A e B , de mesmo comprimento de onda λ , estão inicialmente em fase e se propagam para a direita, como indicam os dois raios. A onda A é refletida por quatro su
Duas ondas sonoras, produzidas por duas fontes diferentes de mesma frequência, 540H z , se propagam na mesma direção e no mesmo sentido a 330m / s . As fontes estão em fase. Qual é a diferença de fase
Na figura, um som com um comprimento de onda de 40,0c m se propaga para a direita através de um tubo que possui uma bifurcação. Ao chegar à bifurcação, a onda se divide em duas partes. Uma parte se pr