Passo 1
Vamos fazer um esboço da situação:
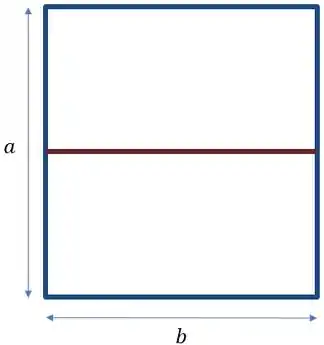
Dado esse esboço, temos o seguinte que o custo vai ser dado pelo custo do comprimento do em volta do terreno (azul) somado ao comprimento no centro (vermelho), o que nos dá:
Onde temos que a área vale sempre , ou seja:
Logo, a função fica
Passo 2
Vamos otimizar a função, derivando-a e igualando a :
O que gera .
Passo 3
Para garantir que esse é um ponto de mínimo, aplicamos o limite de quando . Fazendo isso, veremos que explode para
Somado a isso o fato de que só temos um ponto crítico, temos a certeza que é um ponto de mínimo!
Resposta
Exercícios de Livros Relacionados
Encontre, com precisão de duas casas decimais, as coordenadas do ponto na curva y = tan x que está mais próximo do ponto ( 1,1 )
Resolva o problema no Exemplo 4 se o rio tiver 5k m de largura e o ponto B estiver somente a 5k m de A rio abaixo.
Encontre o ponto sobre a reta y = 4 x + 7 que está mais próximo da origem.
Se 1200c m 2 de material estiverem disponíveis para fazer uma caixa com uma base quadrada e sem tampa, encontre o maior volume possível da caixa.
Um fazendeiro quer cercar uma área de 15000m 2 em um campo retangular e então dividí-lo ao meio com uma cerca paralela a um dos lados do retângulo. Como fazer isso de forma a minimizar o custo da cerc