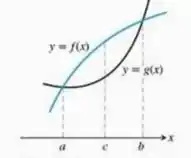
Sejam e as funções deriváveis traçadas aqui. O ponto é onde a distância vertical entre as curvas é máxima. Há algo de especial em relação às tangentes às duas curvas em ? Justifique sua resposta.
Passo 1
Temos que o ponto será um ponto de mínimo da distância entre os dois. Essa distância é puramente vertical, então:
Sendo a distância.
Passo 2
estará presente em um dos pontos críticos. Então vamos derivar:
Passo 3
Pontos críticos ocorrem onde a derivada não existe ou é zero. Ela sempre vai existir, pois e são deriváveis. Então, resta zero:
Passo 4
será o ponto onde as derivadas são iguais. Agora vamos relembrar a equação da reta tangente a cada curva?
Se as derivadas são iguais, as retas tangentes a e diferem apenas da quantidade e . Portanto, elas tem a mesma inclinação, mas diferem na translação, ou seja, são retas paralelas.
Resposta
Retas tangentes paralelas