UFRJ – Cálculo 1 – Lista 13 – Questão 5
Um pedaço de fio com de comprimento é cortado em duas partes. Uma parte é dobrada no formato de um quadrado, ao passo que a outra é dobrada na forma de um triângulo equilátero. Como deve ser cortado o fio de forma que a área total englobada seja: (a) máxima? (b) mínima?
Passo 1
A primeira coisa é esboçar as informações dadas num desenho:
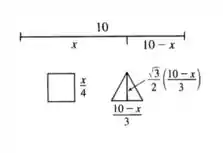
Cada lado do quadrado vale porque o tamanho de fio é dividido pelos quatro lados, e o triângulo usa a mesma lógica. A altura do triângulo possui esse valor por conta da propriedade geométrica que nos dias que .
Passo 2
O exercício quer a área total máxima e mínima dessas figuras, então:
O limite imposto de x entre zero é dez é por conta do tamanho do fio.
Passo 3
Como está dependendo de apenas uma variável, já é possível derivar e igualar a zero para encontrar seus valores extremos:
Passo 4
Como pode variar entre zero e dez, substituímos esses dois valores além do encontrada para encontrar seus valores extremos e achar os pontos máximos e mínimos:
Passo 5
Item (a): área máxima encontrada acontece quando , e vale , ou seja, toda a corda é usada para o quadrado.
Passo 6
Item (b): área mínima encontrada acontece quando , e vale .
Resposta
Item (a): área máxima: .
Item (b): área mínima: .