3. Considere a família de todos os triângulos retângulos como na figura abaixo. Um vértice do triângulo é a origem do plano e a hipotenusa é o segmento de reta tangente ao gráfico da função .
a) Existe um triângulo com área máxima? Justifique sua resposta.
b) Encontre o comprimento da menor hipotenusa desta família de retângulos. Justifique sua resposta.
Passo 1
Oi, galerinha! Tudo bom? Embora o enunciado diga que nos deu uma figura, ele não forneceu para a gente como é essa família de triângulos. Mas ele deu uma informação importante com qual podemos desenhar.
Ele disse que a hipotenusa é o segmento de reta tangente ao gráfico da função . Desenhando , ficamos com
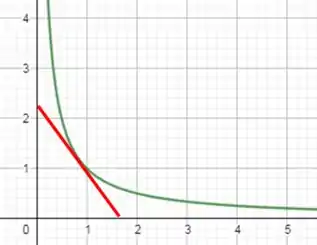
A nossa função esta em verde e a nossa reta tangete está em vermelho. Repara que ela forma um triangula retângulo com os eixos.
Passo 2
- Primeiro temos que verificar se existe um triângulo com área máxima. Ou seja, temos que fazer uma otimização para encontrar a maior área.
- Agora temos que achar o comprimento da menor hipotenusa desta família de retângulos. Para isso, vamos usar a relação que diz que a soma do quadrado dos catetos é igual ao quadrado da hipotenusa.
A área do triangulo é dada por
Onde, é minha base que será dada pelo meu eixo e é a minha altura que será dada pelo eixo .
Para otimizar essa função precisamos estabelecer uma relação entre a base e a altura e vamos fazer isso pela reta tangente (que é a nossa hipotenusa).
Passo 3
Para encontrarmos a reta tangente de uma função utilizamos a seguinte formula:
Temos que . Logo sua derivada será . Substituindo na equação temos:
Ajeitando
Encontramos a equação da reta tangente. Uhuuul!!
Onde é o ponto cuja a reta tangente corta.
Passo 4
Agora que temos a função da reta tangente, vamos calcular a área do triângulo. Pra isso, vamos calcular a altura e a base.
A altura vai ser o ponto em que a reta cruza o eixo , ou seja, vai ser o valor da função no ponto . Então se a gente substituir , vamos achar .
Já a base do triângulo é o valor de , quando a reta cruza o eixo . Então é ponto , quando .
Note que isso vai valer pra qualquer triângulo, pois não definimos nada que especifique qual é a reta tangente. Com isso, a área do triangulo sempre será
Olha só, é um valor constante! Como os termos se cancelaram, isso significa que a área não depende do ponto que a reta tangente toca a curva.
Concluimos então que não há uma área máxima.
Passo 5
Como na letra a vimos que a base e a altura serão sempre será e . Então fica assim,
Para achar o menor comprimento, vamos otimizar essa formula e a gente faz isso achando os pontos críticos. Pra achar os pontos críticos, vamos derivar e igualar a zero.
Resolvendo pra
Repara que se a gente minimizar o quadrado da hipotenusa , a gente automaticamente minimizaa hipotenusa ne.
Substituindo na fórmula da hipotenusa ficamos com
Resposta
- Não há máximo.