Encontre as dimensões de um retângulo com um perímetro de cuja área seja a maior possível.
Passo 1
É um problema de maximização. Temos que maximizar a função área. O problema nos deu o perímetro.
Vamos seguir o passo a passo para problemas de otimização.
1º Passo: Deve-se desenhar o problema e anotar as condições dadas, o que é super importante para um melhor entendimento do problema.
.
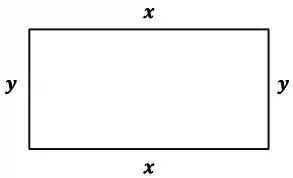
Passo 2
2º Passo: Temos que escrever equações que relacionam as variáveis do problema. Nesse passo, podem ser necessários conhecimentos básicos de geometria, trigonometria, etc.
O perímetro vai ser:
E a área:
Passo 3
3º Passo: Analisando as equações, chegamos na função que desejamos otimizar em função de apenas uma variável.
Queremos maximizar a função área :
Passo 4
4º Passo: ivamos essa função e achamos os pontos críticos.
Passo 5
5º Passo: Analisamos os sinais das derivadas antes e depois dos pontos críticos para garantir que sejam máximo ou mínimo.
Vamos analisar a função:
Repare que a função é um polinômio de segundo grau e, portanto, é uma parábola voltada para baixo e só possui um ponto de máximo, que é o que achamos anteriormente. Logo:
Não precisamos de outros passos aqui, pois, por ser uma parábola voltada para baixo, esse é um ponto de máximo global.
Resposta
Trata-se de um quadrado de lado igual a .