Sejam e pontos contidos no eixo e eixo , respectivamente, tais que o segmento ligando e passa por . Determine e tal que a área do triângulo com vértices e é mínima.
Passo 1
Vamos começar entendendo essa situação, fazendo aquele clássico esboço!
Queremos estudar os triângulos cujos 3 vértices estão:
- um na origem
- um no eixo (ponto )
- um no eixo (ponto )
Sendo que o segmento que liga e passa por . Então seria algo assim:
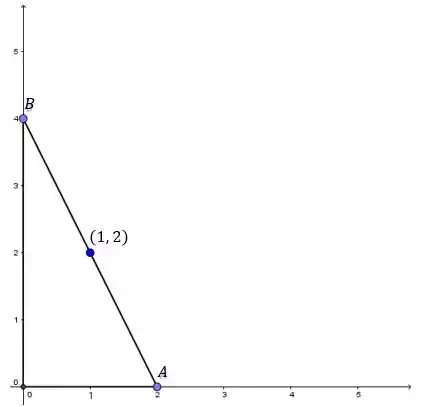
Variando os pontos e , a gente pode obter infinitos triângulos:
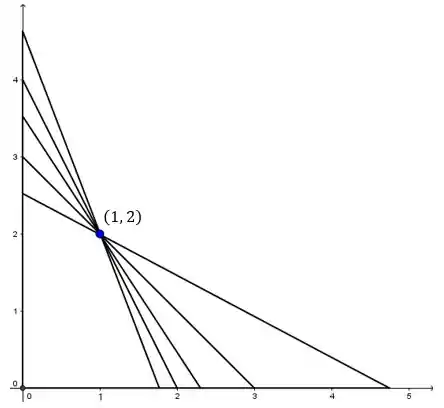
E desses triângulos todos, queremos o de menor área!
Passo 2
Agora que fizemos o esboço, vamos nomear as variáveis do problema.
O que varia é a posição de e a posição de . Mas está sempre no eixo e no eixo . Então digamos que as coordenadas de e são
Assim e serão nossas variáveis: respectivamente, a base e a altura do triângulo.
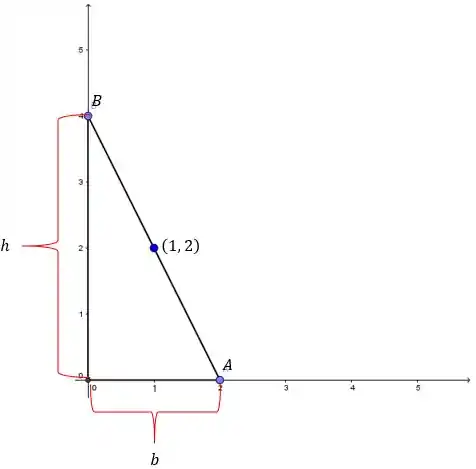
Portanto, a área do triângulo é dada por:
Passo 3
Agora vejamos qual é a relação entre e . Tive uma ideia meio louca pra fazer isso, vê o que você acha.
Conhecemos 3 pontos que fazem parte do segmento que liga e : e , certo? E esse segmento tem um certo coeficiente angular que, como todo bom coeficiente angular, pode ser encontrado a partir de apenas 2 pontos.
Então vamos fazer o seguinte: encontrar esse coeficiente angular em função de , e depois em função de , e igualar os dois! Beleza?
Usando os pontos e , temos que o coeficiente angular da reta é:
Usando os pontos e :
Passo 4
Agora é só igualar os 2 resultados pra achar uma relação entre e :
Isolando o :
Pronto, achamos em função de :)
Passo 5
Estamos interessados na área do triângulo:
Substituindo
Achamos:
Ou, se preferir:
Queremos o triângulo de área minimal então nossa missão vai ser achar o mínimo global dessa função , show?
Passo 6
Antes de partirmos pra achar esse mínimo global, vamos só parar rapidinho pra determinar o domínio da função . Esse é um detalhe que pode vir a ser muito importante.
pode ser o quão grande a gente quiser, não tem problema aumentar ele que o triângulo ainda vai existir de boa.
Agora, repare que devemos ter . Senão não daria pra fechar um triângulo passando pelo ponto . Olhando na figura isso fica mais claro.
Enfim, isso significa que o domínio de é o intervalo .
Dito isso, vamos continuar!
Passo 7
Vamos derivar essa função área pra achar seus pontos críticos. Pela regra do quociente:
Igualando a derivada a zero:
Ou seja:
Mas está fora do domínio de , logo:
Esse é o único ponto crítico da função .
Passo 8
Vamos analisar o sinal da derivada pra determinar se esse ponto é mesmo o ponto de mínimo global que procuramos.
Montando o famoso quadro de sinais (lembrando que ):
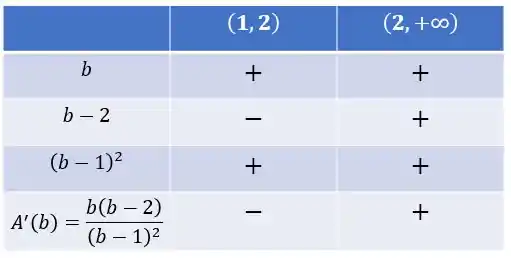
No intervalo a derivada é negativa, então a área dos triângulos vai diminuindo. Depois, com , a área passa a aumentar.
Então sim, o ponto é o ponto de mínimo global da função .
Passo 9
Estamos quase acabando! Concluímos que o triângulo de menor área tem base , então sua altura vai ser:
Portanto, os pontos e que minimizam a área do triângulo são:
Aee matamos a questão! :)