Seja uma função diferenciável em todos os pontos de e
Considere a seguinte tabela de valores:
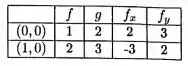
Quanto valem e , respectivamente?
Passo 1
Temos
Então
Para achar essas derivadas parciais, vamos usar a regra da cadeia:
Passo 2
Vamos começar então calculando as derivadas parciais de e de que é a única coisa que vamos conseguir calcular. O resto teremos que olhar na tabela.
As derivadas parciais de são:
E as derivadas parciais de são:
Substituindo no ponto , temos
Passo 3
Agora é só substituir na fórmula da regra da cadeia. Mas fica ligado que é função de e quando ,
Substituindo os valores que encontramos no passo 2 e os valores da tabela: