Segunda Lei da Termodinâmica
Marque a alternativa que mostra a desigualdade correta para o ciclo mostrado na figura. Os valores e representam os MÓDULOS dos calores trocados pelo ciclo com cada reservatório térmico.
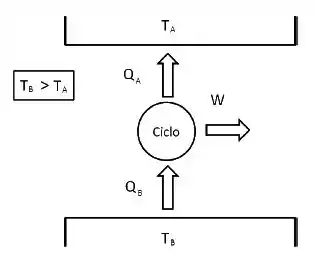
Passo 1
Essa questão é bem capciosa. É preciso tomar cuidado com uma coisa:
A variação de entropia de um ciclo é igual a zero, mas variação do ambiente ao seu redor não necessariamente será.
Vamos analisar as opções então, mas antes, vamos calcular uma expressão pra variação de entropia de um sistema nas redondezas de um ciclo:
Como :
Podemos esperar que pra uma fonte fria e uma quente, apenas, teremos:
Onde os índices se referem à fonte fria e os índices à fonte quente.
Passo 2
Mas como sempre, sabemos que a entropia de um sistema só aumenta ou se mantêm constante, ou seja, a a variação de entropia é maior que zero ou igual à zero.Logo:
Passo 3
Beleza, então vemos que é resposta seria a letra a).
Mas no gabarito a b) também é tida como correta. Por quê?
Bom, provavelmente erraram ao incluir essa opção, mas ela é sim uma verdade, por um simples motivo: O enunciado nos diz que os calores envolvidos são módulos de calores.
Isso quer dizer que são sempre positivos. E como as temperaturas são dadas em kelvins, os quocientes são positivos. Logo, como a soma de dois números não negativos é sempre maior ou igual a zero, temos que:
Resposta
a)
b)