Exercícios de Variação da Entropia de um Gás Ideal - Lista de Exercícios Resolvida
Questão 1
Num processo de expansão livre de um gás ideal isolado do ambiente:
A energia interna do gás aumenta e a entropia fica a mesma.
A energia interna e a entropia do gás ficam as mesmas.
A energia interna do gás diminui e a entropia fica a mesma.
A energia interna e a entropia do gás aumentam.
A energia interna do gás fica a mesma e a entropia aumenta.
A energia interna do gás diminui e a entropia aumenta.
A energia interna e a entropia do gás diminuem.
Ver solução completaQuestão 2
Um recipiente rígido (volume constante) e isolado termicamente contém de nitrogênio na forma de gás a pressão de e a temperatura de . Um agitador mecânico, com pás no interior do recipiente, realiza de trabalho sobre o gás. O calor específico do nitrogênio, a volume constante, é .
Calcule a temperatura final do gás.
Calcule a variação de entropia do universo neste processo.
Ver solução completaQuestão 3
Um gás ideal diatômico descreve o ciclo definido pelas seguintes etapas:
: processo a volume constante , desde a pressão até .
: expansão a pressão constante , do volume até .
: processo a volume constante , de até .
: compressão a pressão constante , de até .
Desenhe o ciclo num gráfico versus , sendo Pa e
Dado que o número de mols do gás é tal que , calcule a temperatura em cada vétice.
Obtenha o trabalho realizado pelo gás em cada ciclo.
Obtenha o calor trocado em cada etapa do ciclo, indicando se é recebido ou cedido pelo gás.
Calcule a eficiência de um motor térmico operando segundo o ciclo .
Calcule a variação de entropia da etapa e a variação de entropia no ciclo completo.
Ver solução completaQuestão 4
Uma máquina térmica operando entre as temperaturas e rejeita
para a fonte fria uma quantidade de calor em um ciclo. Sua eficiência é igual a
da eficiência máxima (Carnot) para essas fontes.
Calcule a quantidade de calor fornecida pela fonte quente e o trabalho realizado em cada ciclo.
Qual deve ser a duraçãoo de cada ciclo para que a potencia média que a máquina entrega seja igual a ?
Essa mesma máquina é utilizada para alimentar um refrigeradore que retira, a cada ciclo (da mesma duraçãoo que o da máquina), uma certa quantidade de calor de um compartimento à temperatura , despejando no ambiente, a uma temperatura , uma quantidade de calor .
Faça um esquema do funcionamento do sistema composto,indicando com setas os fluxos de energia.
Sendo , obtenha o coeficiente de desempenho do refrigerador.
Calcule a variação de entropia do sistema [refrigerador compartimento a ambiente a ] após um ciclo. O resultado é compatível com a segunda lei da termodinâmica?
Ver solução completaQuestão 5
Um mol de um gás ideal monoatômico, inicialmente à pressão e temperatura de expande a partir de um volume inicial até . Durante a expansão a pressão e o volume do gás estão relacionados pela expressão:
Onde está em ·, e em unidades de , e . Determine:
A pressão final
A temperatura final
Qual o trabalho realizado pelo gás durante a expansão
Qual a variação de entropia do gás durante a expansão?(dica: Use dois processos reversíveis simples ligando os estados inicial e final para calcular a variação de entropia).
Dados:
Ver solução completaQuestão 6
O ciclo da figura abaixo representa a operaçãoo de um motor de combustão interna de gasolina (ciclo de Otto). Suponha que a mistura gasolina-ar é equivalente a mols de um gás ideal com .
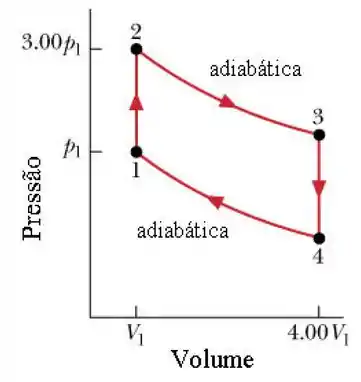
Determine as razões entre as temperaturas absolutas , e .
Determine as razões entre as pressões e .
Determine o trabalho total realizado no ciclo (em função de ).
Em que fase o calor é fornecido ao sistema? Calcule esse calor (em função de ).
Calcule a eficiência dessa máquina, supondo que todas as trocas de calor ocorrem com fontes externas ao sistema.
Determine a variação de entropia da substância de trabalho em cada fase do ciclo (em função de ).
Ver solução completaQuestão 7
Duas amostras de um gás à mesma temperatura e pressão, são comprimidas do volume para um volume , uma isotermicamente e outra adiabaticamente.
Determine a pressão final nos dois casos
Determine a variação de entropia nos dois casos.
Ver solução completaQuestão 8
Uma máquina térmica opera entre dois reservatórios a e . Ela absorve de calor do reservatório de temperatura mais elevada e executa de trabalho durante um ciclo. Encontre, com justificativas:
A variação da entropia da máquina em um ciclo e a variação da entropia do universo para este processo.
O trabalho feito por uma máquina de Carnot que opera entre esses dois reservatórios absorvendo de calor da fonte de temperatura mais elevada.
Ver solução completaQuestão 9
Um mol de gás ideal monoatômico, partindo sempre do estado inicial de volume , pressão e temperatura , dobra a temperatura por quatro processos diferentes. O processo é a volume constante, o processo é isobárico, o é linear com pressão final e é adiabático. Dê as respostas em função de , e .
Coloque na tabela os valores da pressão e do volume no final de cada processo. Represente cada processo no diagrama .
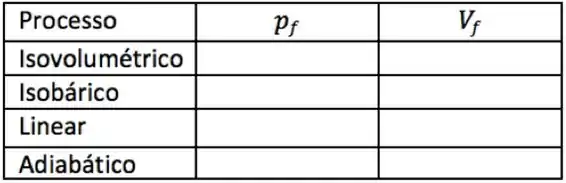
Calcule a variação da energia interna para cada um dos processos.
No processo , calcule o trabalho e o calor trocado.
Calcule o trabalho realizado e a variação de entropia nos processos e .
Ver solução completaQuestão 10
A máquina térmica de um inventor opera entre duas fontes térmicas, uma quente à temperatura e outra, fria, à temperatura . Cada ciclo dessa máquina dura , recebendo de calor da fonte quente, por ciclo.
Suponha que uma máquina de Carnot funcionando entre essas duas fontes tenha eficiência . Calcule a temperatura da fonte fria
A eficiência da máquina térmica do inventor vale da eficiência da máquina térmica de Carnot mencionada em . Obtenha a eficiência da máquina do inventor e o trabalho realizado a cada ciclo. Calcule ainda a potência da máquina.
Com relação à máquina térmica do inventor, determine, por ciclo, o calor rejeitado para a fonte fria, avariação da entropia da fonte fria e a variação de entropia do conjunto máquina térmica, fonte quente e fonte fria.
Se acloparmos um refrigerador (não é de Carnot), com coeficiente de desempenho , recebendo o trabalho realizado pela máquina térmica do inventor, calcule o calor retirado pelo refrigerador da fonte fria e o calor rejeitado para a fonte quente (por ciclo).
Ver solução completaQuestão 11
Marque a alternativa que mostra a desigualdade correta para o ciclo mostrado na figura. Os valores e representam os MÓDULOS dos calores trocados pelo ciclo com cada reservatório térmico.
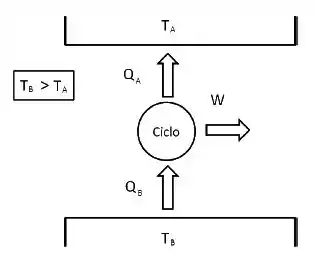
Questão 12
Uma máquina térmica opera entre dois reservatórios a e . Ela absorve de calor do reservatório de temperatura mais elevada e executa de trabalho durante um ciclo. Encontre, com justificativas:
- A variação da entropia da máquina em um ciclo e a variação da entropia do universo para este processo.
- O trabalho feito por uma máquina de Carnot que opera entre esses dois reservatórios absorvendo de calor da fonte de temperatura mais elevada.
Questão 13
Uma máquina térmica opera entre dois reservatórios a e . Ela absorve de calor do reservatório de temperatura mais elevada e executa de trabalho durante um ciclo. Encontre COM JUSTIFICATIVAS:
- A variação de entropia da máquina e a variação de entropia do universo para este processo.
- O trabalho feito por uma maquina de Carnot que opera entre esses dois reservatórios absorvendo de calor da fonte de temperatura mais elevada.
- O trabalho desperdiçado, isso é, a diferença entre o trabalho realizado pela presente máquina e o trabalho feito por uma máquina de Carnot que opera entre as mesmas temperaturas.
Questão 14
Um mol de gás ideal monoatômico realiza o ciclo mostrado no diagrama abaixo. No ponto o estado do gás é descrito por , e .
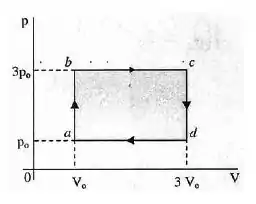
- Em que etapas do ciclo o gás recebe calor da vizinhança, e qual é o calor total recebido?
- Em que etapas do ciclo o gás cede calor para a vizinhança, e qual é o calor total cedido?
- Qual é o rendimento de um motor operando neste ciclo?
- Qual é a variação da entropia do gás no processo ?
Adote: e .
Ver solução completaQuestão 15
Um recipiente rígido (volume constante) e isolado termicamente contém de nitrogênio na forma de gás a pressão de e a temperatura de . Um agitador mecânico, com pás no interior do recipiente, realiza de trabalho sobre o gás. O calor específico do nitrogênio, a volume constante, é .
a) Calcule a temperatura final do gás.
b) Calcule a variação de entropia do universo neste processo.
Ver solução completaQuestão 16
A operação de um motor a gasolina a combustão interna está representado pelo ciclo abaixo cuja a eficiência é Suponha que a mistura gasolina + ar seja um gás ideal com moles. Expresse suas respostas em termos de , , e
- Qual a pressão no ponto 3?
- Qual a energia adicionada ao gás na forma de calor?
- Qual o trabalho resultante realizado pelo gás em termos de eficiência do ciclo?
- Qual a variação de entropia do ciclo?

Questão 17
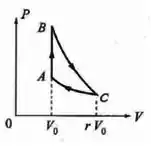
Numa máquina térmica, o agente é um mol degás ideal de coeficiente adiabático, que executa o ciclo da figura abaixo, onde BC é uma adiabática e CA uma isoterma.Definindo =,= e = , em termos de r, , , e :
a) Calcule PC;
b) Calcule PB;
c) Calcule TB;
d) Calcule o trabalho no processo BC;
e) Calcule a variação da entropia do gás no processo CA.
Observação: Qualquer resultado que não esteja fornecido no formulário em anexo deve ser DEMONSTRADO.
Questão 18
Um mol de gás diatômico ideal tem seu estado inicialicaracterizado por uma pressão e um volume . O gás é aquecido através de dois processos termodinâmicos. O primeiro processo é a volume constante e o segundo a pressão constante. O estado termodinâmico final f do gás é caracterizado por uma pressão 3 vezes maior do que a inicial e um volume 2 vezes maior do que o inicial. Considere que as temperaturas envolvidas nos processos não ativam graus de liberdade vibracionais do gás. Dê suas respostas em termos de, e R, a constante dos gases ideais.
a) Desenhe o diagrama P-V indicando claramente o estado final e o inicial do gás e sua trajetória de processos termodinâmicos.
b) Calcule a quantidade de calor absorvida ou retirada pelo gás ao ir de seu estado inicial i ao final f.
c) Calcule a variação da entropia do gás ao ir do estado inicial i ao final f.
Observação: Qualquer resultado que não esteja fornecido no formulário em anexo deve ser DEMONSTRADO.
Ver solução completaQuestão 19
A figura mostra o diagrama pressão x volume do ciclo termodinâmico a que é submetido de um gás ideal poliatômico. As setas indicam o sentido do ciclo. Na figura , e
Para os itens (a), (b) e (c) assuma que a curva é isotérmica.
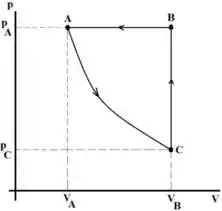
- Calcule o valor de e .
- Calcule o trabalho realizado pelo gás no ciclo.
- Calcule a variação de entropia na trajetória .
- Calcule o valor de e .
- Calcule o valor do trabalho feito no ciclo.
- Calcule a variação de entropia na trajetória
Para os itens (d), (e) e (f) assuma que a curva é adiabática.
Dados:
Ver solução completaQuestão 20
Considere que um mol de um gás ideal se expande até dobrar de volume isotermicamente a temperatura e outro mol do mesmo gás, também a temperatura , dobra de volume através de uma expansão livre. Sobre esses dois processos, são feitas as seguintes assertivas:
- O trabalho realizado em ambos os processos pode ser calculado através da expressão , onde é a pressão do gás e , o seu volume.
- A variação de entropia do gás é a mesma nos dois processos e é dada pela expressão .
- O calor recebido pelo gás em ambos os processos pode ser calculado pela expressão .
- A variação de entropia do gás nos dois processos é ; logo, ambos os pro essos são irreversíveis.
- Em ambos os processos, o estado final atingido pelo gás é diferente do inicial; logo, a variação de energia interna do gás nos dois necessariamente deve obedecer .
São verdadeiras:
(a) Apenas I e II.
(b) Apenas a II.
(c) Apenas I, II e III.
(d) Apenas II e IV.
(e) Apenas a V.
(f ) Apenas III, IV e V.
(g) Apenas I, II e IV.
Ver solução completaQuestão 21
O gráfico X a seguir mostra como o volume de um mol de um gás ideal varia com a pressão ao longo de dois processos e .Sobre esses processos, é correto afirmar que
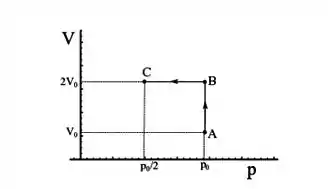
- A variação da energia ao longo de todo o processo é nula.
- O trabalho realizado pelo gás é nulo no processo .
- No processo , o gás recebeu uma quantidade de calor equivalente a .
- A variação de temperatura é negativa no processo .
- No processo , o gás perde calor e uma quantidade positiva e não-nula de trabalho é realizada sobre ele.
- A variação de entropia no processo é nula, pois o processo é reversível.
Questão 23
Dois gases ideais idênticos, e , de mesmo volume inicial , se expandem, aumentando seu volume de uma mesma quantidade . O gás expande-se livremente e em isolamento térmico, enquanto o gás expande-se lentamente, realizando trabalho e sem que sua temperatura varie. Julgue as seguintes alternativas:
I. O gás não realiza trabalho ao se expandir.
II. A variação de entropia é igual em ambos os casos.
III. O gás têm sua temperatura reduzida por conta da expansão.
IV. A variação de entropia em é maior do que a variação de entropia em .
V. A expansão de não causa o aumento de sua entropia, pois o processo é reversível.
(a) Apenas I está correta.
(b) Apenas II está correta.
(c) Apenas I e II estão corretas.
(d) Apenas I e V estão corretas.
(e) Apenas IV e V estão corretas.
(f) Apenas III e IV estão corretas.
(g) Apenas III, IV e V estão corretas.
Ver solução completaQuestão 24
Um gás ideal cujo calor específico é , realiza o ciclo representado no diagrama na figura.
Considere
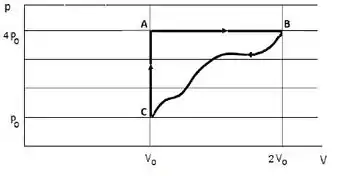
(a) Calcule as temperaturas nos pontos de funcionamento do ciclo
(b) Se o trabalho realizado pelo gás em cada ciclo é , calcule o trabalho no trecho , explicitando se é realizado ou recebido pelo gás.
(c) A eficiência deste sistema operando como uma máquina térmica é 0,06. É compatível este resultado com o esperado de acordo com a segunda lei da termodinâmica? (compare a eficiência com a de uma máquina de Carnot funcionando entre as mesmas temperaturas extremas).
(d) Para cada ciclo, determine o calor que deve ser fornecido ao gás e o calor que o sistema perde.
(e) Qual é a variação de entropia do gás no processo BC?
(f) Este gás é monoatômico, diatômico ou poliatômico? Justifique.
Ver solução completaQuestão 25
O ciclo da figura abaixo representa a operação de um motor de combustão interna a gasolina. O volume . Suponha que a mistura de admissão gasolina-ar seja de um gás ideal () e com .
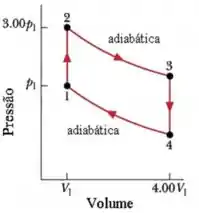
- Determine as razões
- Determine as razões,.
- Calcule a eficiência deste motor.
- Calcule a variação de entropia para os processos .
Questão 26
A respeito da entropia de um gás, analise a alternativa INCORRETA:
- Se o gás é resfriado a volume constante, sua entropia diminui.
- Se o gás se expande a temperatura fixa, sua entropia aumenta.
- Se o gás realiza um ciclo irreversível, sua entropia aumenta.
- A entropia do gás não se altera em uma expansão adiabática reversível.
Questão 27
Considere a quantidade , onde é a energia interna de um gás ideal, a sua temperatura e a sua entropia. Numa expansão adiabática livre podemos afirmar que a variação de será:
(a) Negativa, pois a energia interna e a temperatura do gás são constantes e a entropia aumenta.
(b) Negativa, pois a temperatura do gás é constante e a energia interna e a entropia aumentam.
(c) Nula, pois a energia interna, a temperatura e a entropia do gás permanecem constantes.
(d) Nula, pois a varação da energia interna do gás é positiva, a temperatura é constante e a variação da entropia é positiva de tal forma que . (e) Positiva, pois a energia interna e a temperatura do gás permanecem constantes e sua entropia diminui.
Ver solução completaQuestão 28
Sobre a segunda lei da termodinâmica e alguns processos termodinâmicos, assinale V (verdadeiro) ou F (falso) nas afirmações a seguir:
1. ( ) A entropia de processo reversível em um sistema fechado tem uma variação maior do que zero.
2. ( ) A entropia pode diminuir para um sistema aberto em um processo irreversível.
3. ( ) A entropia, sendo uma forma de energia, se conserva em sistemas fechados, mas pode variar de acordo com o estado termodinâmico.
4. ( ) A geladeira pode resfriar a cozinha se for deixada com a porta aberta.
5. ( ) A energia interna de um gás ideal que é comprimido isotermicamente não muda durante o processo.
6. ( ) No processo de expansão livre de um gás ideal, a temperatura após a expansão é superior `a temperatura antes da expansão.
Ver solução completaQuestão 29
. O ciclo de Brayton é uma representação dos processos térmicos que ocorrem nas turbinas a gás, como as usadas na aviação. Suponhamos que se trata de moles de um gás ideal com . O ciclo se divide em etapas, incluindo uma compressão e uma expansão adiabáticas reversíveis, como mostra a figura abaixo:
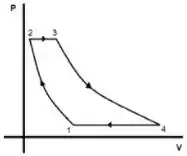
Calcule a variação da entropia em cada etapa do ciclo.
Ver solução completaQuestão 30
Um sistema é composto por moles de um gás ideal monoatômico. O volume inicial é igual a .
a) A variação de energia interna deste sistema para ir de um estado inicial com volume inicial até o estado final com volume final é de . Determine o trabalho, a quantidade de calor fornecida ou retirada do sistema e a variação da entropia se o processo reversível para ir do estado até o estado é uma adiabática.
b) Determine o trabalho, a quantidade de calor fornecida ou retirada do sistema e a variação de entropia se o processo reversível para ir do estado até o estado for feito a uma pressão constante de e o volume inicial é de .
c) Determine o trabalho, a quantidade de calor fornecida ou retirada do sistema e a variação de entropia se o processo reversível para ir do estado até o estado é uma isoterma com temperatura .
Ver solução completaQuestão 31
A figura abaixo é o diagrama do ciclo de uma máquina que faz uso de de um gás ideal monoatômico. Os processos são adiabáticos, enquanto são processos a pressão constante (isobáricas). Sejamas temperaturas nos estados , respectivamente. Para as questões abaixo, expresse seu resultado em termos das temperaturas, da constante dos gases, , e do número de moles, .
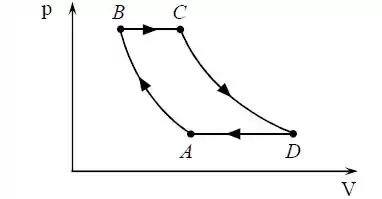
- Calcule o calor trocado em cada etapa do ciclo e o trabalho total realizado no ciclo.
- Calcule a eficiência de uma máquina operando neste ciclo fazendo uso de um gás ideal.
- Calcule a variação da entropia do gás em cada etapa do ciclo.
Questão 32
Considere as seguintes afirmativas:
I. Na expansão livre de um gás ideal, que passa de um volume para um volume , a temperatura e a energia interna permanecem as mesmas, mas a entropia aumenta;
II. Na expansão lenta de um gás ideal ao longo de uma isoterma não há troca de calor e a entropia permanece constante;
III. Quando dois corpos inicialmente em temperaturas diferentes são colocados em contato térmico, mantidos isolados do resto do universo, o calor total trocado entre os corpos é nulo e a entropia não varia;
IV. Na expansão lenta de um gás ideal ao longo de uma adiabática não há troca de calor e a entropia do gás permanece constante;
V. A passagem de um sistema isolado de um estado de menor entropia para outro de maior entropia é um processo irreversível;
Podemos afirmar que são verdadeiras as afirmativas:
Questão 33
A figura ao lado mostra um ciclo reversível ao qual são submetidos de um gás ideal monoatômico. No ponto a pressão e o volume são e e no ponto são e respectivamente. Analise as afirmações abaixo:
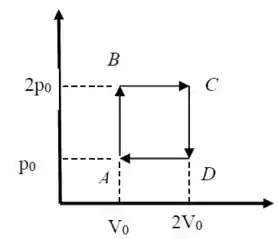
I)A temperara
II) O calor recebido pelo sistema no processo é
III)A eficiência de um ciclo de Carnot que operasse entre as temperaturas mais baixa e mais alta do ciclo mostrado na figura seria .
IV) A eficiência no ciclo da figura é menor que
V)A variação da entropia no processo é
Assinale a alternativa correta:
a) Somente as afirmações I e III são falsas.
b)A afirmações I, IV e V são falsas.
c)As afirmações I, II, III são verdadeiras.
d)Somente a afirmações I e II são verdadeiras.
e)Todas as afirmações são verdadeiras
Ver solução completaQuestão 34
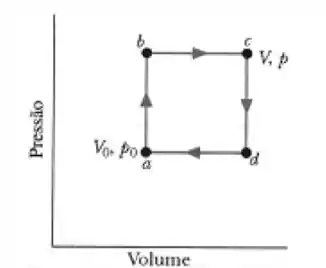
Um mol de um gás ideal monoatômico percorre o ciclo mostrado na figura ao lado. Em c a pressão e o volume são respectivamente e . e são o volume e a pressão em a. Analise as afirmações abaixo:
(I)A temperatura .
(II) A variação da entropia no processo abc é .
(III)A eficiência da máquina que opera com este ciclo é de
(IV). A eficiência de um ciclo de Carnot operando entre as temperaturas mais alta e mais baixa é de .
(V) .
São afimarções verdadeiras:
- Somente III, IV e V
- Somente III e V.
- Somente I e III.
- Todas
- Somente I, III, IV e V.
Questão 35
Assinale a alternativa correta:
Num processo de expansão livre de um gás ideal isolado do ambiente:
- A energia interna do gás aumenta e a entropia fica a mesma.
- A energia interna e a entropia do gás ficam as mesmas.
- A energia interna do gás diminui e a entropia fica a mesma.
- A energia interna e a entropia do gás aumentam.
- A energia interna do gás fica a mesma e a entropia aumenta.
- A energia interna do gás diminui e a entropia aumenta.
- A energia interna e a entropia do gás diminuem.
Questão 36
O ciclo de Joule, representado na figura abaixo, onde e são adiabáticas, é uma idealização do que ocorre em uma turbina de gás: e representam respectivamente aquecimento e resfriamento à pressão constante; é a taxa de compressão e . Seja o coeficiente adiabático do gás ideal submetido ao ciclo dado por .
Dados: , e
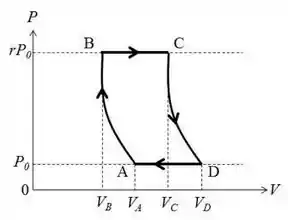
- Calcule o calor trocado no processo () em termos de , , e
- Calcule o calor trocado no processo () em termos de , e
- Usando os resultados do item anterior, calcule o rendimento do ciclo em termos de e
- Sabendo que mols do referido gás são usados na turbina, calcule a variação de entropia no processo em termos de e
Questão 37
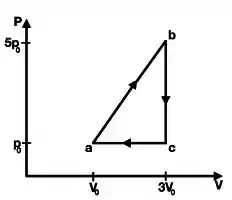
Um mol de gás ideal monoatômico (= 3R/2) realiza um ciclo termodinâmico reversível, como mostrado na figura ao lado. Note que o processo ab é a única etapa em que o gás absorve calor no ciclo, enquanto que sua pressão varia linearmente durante esta expansão. Nos tempos bc e ca o gás libera calor. Determine:
a) O trabalho total realizado pelo gás no ciclo.
b) A eficiência do ciclo.
c) A variação de entropia do gás no processo bc e justifique porque seu resultado não viola a segunda lei da termodinâmica.
Questão 38
Um cilindro conectado a um pistão contém um gás ideal em equilíbrio térmico com temperatura T, volume V e pressão P. Este cilindro está imerso em um reservatório térmico com a mesma temperatura T e o pistão acoplado pode ser movido lentamente ou bruscamente, causando uma variação de volume V, que pode ser positiva ou negativa. A parede do cilindro pode ser de material condutor ou isolante térmico, o que vai determinar a natureza do processo termodinâmico sofrido pelo gás. Para os cinco processos termodinâmicos descritos de acordo com a variação do volume, movimento do pistão e material das paredes do cilindro:
i. V > 0, lento, condutor
ii. V > 0, lento, isolante
iii. V > 0, rápido, isolante
iv. V > 0, rápido, condutor
v. V
Assinale a alternativa correta:
(a) O processo I equivale a uma expansão livre adiabática:
(b) O processo II equivale a uma expansão adiabática:
(c) O processo III equivale a uma expansão isotérmica:
(d) O processo IV equivale a uma expansão livre isotérmica:
(e) O processo V equivale a uma compressão livre isotérmica:
(f) O processo III equivale a uma expansão adiabática:
Ver solução completaQuestão 39
Um gás ideal realiza um ciclo de Carnot. A expansão isotérmica ocorre a e a compressão isotérmica ocorre a . O gás absorve de calor do reservatório quente durante a expansão isotérmica. Encontre:
- O calor rejeitado para o reservatório frio em cada ciclo.
- O trabalho realizado pelo gás em cada ciclo.
- Em termodinâmica, é comum utilizar-se de uma grandeza denominada energia livre de Helmotz, definida como . Qual a variação desta grandeza num ciclo completo de Carnot?
Questão 40
O que podemos afirmar sobre a substância de trabalho no ciclo de Carnot?
(a) Sua entropia é constante ao longo de cada etapa isotérmica.
(b) Sua entropia é constante ao longo de cada etapa adiabática.
(c) Sua entropia é proporcional ao inverso da temperatura ao longo de cada etapa adiabática.
(d) Sua variação de entropia no ciclo é positiva.
(e) Sua variação de entropia nas etapas adiabáticas é positiva.
Ver solução completaQuestão 41
A figura mostra o diagrama de um ciclo formado por uma isocórica, uma adiabática e uma isoterma, percorrido no sentido . Marque a afirmativa correta a respeito deste ciclo:
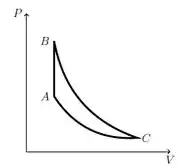
- A variação da entropia é nula de C para A
- A variação da entropia é nula de B para C
- A variação da energia interna é nula de B para C
- A variação da energia interna é negativa de A para B
- No ciclo completo ABCA o sistema perdeu calor
Questão 42
Assinale a afirmação incorreta:
(a) A entropia do gás ideal na expansão livre adiabática aumenta.
(b) O trabalho feito por um gás ideal na expansão livre adiabática é nulo.
(c) A energia do gás ideal é proporcional a .
(d) A temperatura do gás ideal não muda na expansão livre adiabática.
(e) Para o gás ideal temos para a energia interna que
Ver solução completaQuestão 43
Em uma máquina térmica reversível, um mol de um gás ideal monoatômico sofre uma transformação cíclica representada no diagrama pressão-volume da figura abaixo. O processo termodinâmico é isocórico, o é adiabático e o é isobárico.
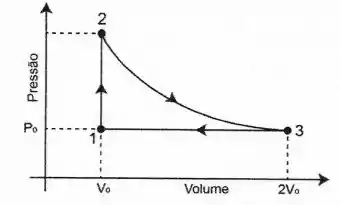
- Calcule a variação de entropia para o ciclo completo.
- Calcule as variações de entropia , e para cada um dos processos. Quando possível, expresse seus resultados em termos de (constante universal dos gases).
- Sabendo que a pressão no estado 1 é , calcule a pressão no estado 2. Expresse seu resultado em termos de .
Questão 44
Uma amostra com moles de um gás ideal com calor específico molar a volume constante é levado de um estado com temperatura e volume a outro , com volume , sendo , através de um processo adiabático reversível.
a) Calcule o trabalho feito pelo sistema durante o processo.
b) Calcule a variação da entropia durante o processo.
Ver solução completaQuestão 45
Um mol de um gás ideal monoatômico é levado do estado inicial com volume e temperatura ao estado final com volume e temperatura por um processo irreversível. A variação da entropia neste processo vale:
(a
(b)
(c)
(d)
Ver solução completaQuestão 46
Uma máquina térmica operando entre as temperaturas e rejeita
para a fonte fria uma quantidade de calor em um ciclo. Sua eficiência é igual a
da eficiência máxima (Carnot) para essas fontes.
Calcule a quantidade de calor fornecida pela fonte quente e o trabalho realizado em cada ciclo.
Qual deve ser a duraçãoo de cada ciclo para que a potencia média que a máquina entrega seja igual a ?
Essa mesma máquina é utilizada para alimentar um refrigeradore que retira, a cada ciclo (da mesma duraçãoo que o da máquina), uma certa quantidade de calor de um compartimento à temperatura , despejando no ambiente, a uma temperatura , uma quantidade de calor .
Faça um esquema do funcionamento do sistema composto,indicando com setas os fluxos de energia.
Sendo , obtenha o coeficiente de desempenho do refrigerador.
Calcule a variação de entropia do sistema [refrigerador compartimento a ambiente a ] após um ciclo. O resultado é compatível com a segunda lei da termodinâmica?
Ver solução completaQuestão 47
Um gás ideal diatômico descreve o ciclo definido pelas seguintes etapas:
: processo a volume constante , desde a pressão até .
: expansão a pressão constante , do volume até .
: processo a volume constante , de até .
: compressão a pressão constante , de até .
Desenhe o ciclo num gráfico versus , sendo Pa e
Dado que o número de mols do gás é tal que , calcule a temperatura em cada vétice.
Obtenha o trabalho realizado pelo gás em cada ciclo.
Obtenha o calor trocado em cada etapa do ciclo, indicando se é recebido ou cedido pelo gás.
Calcule a eficiência de um motoe térmico operando segundo o ciclo .
Calcule a variação de entropia da etapa e a variação de entropia no ciclo completo.
Ver solução completaQuestão 48
A temperatura de duas amostras idênticas do mesmo gás é aumentada da mesma temperatura inicial para a mesma temperatura final em dois processos reversíveis. O processo é executado a volume constante e o processo é executado a pressão constante. A variação da entropia:
a) é maior no processo ;
b) é maior no processo ;
c) é a mesma nos dois processos;
d) é maior no processo apenas se a temperatura inicial for baixa;
e) é maior no processo apenas se a temperatura inicial for elevada;
Ver solução completaQuestão 49
Suponha que queremos dobrar a temperatura de uma certa amostra de gás ideal e temos duas maneiras de realizar isso partindo do mesmo estado inicial, mas chegando a estados finais diferentes: através do processo A, que ocorre de forma reversível a volume constante, ou através do processo B, que ocorre de forma reversível a pressão constante. Podemos dizer que o módulo da variação de entropia
é o mesmo nos dois processos.
é maior no processo A.
é maior no processo B
é nulo em B.
é maior em A apenas se o gás for poliatômico.
é maior em B apenas se o gás for poliatômico.
Ver solução completaQuestão 50
(Cap 20 – Ex 31) a) calcule a variação de entropia quando de água a é vaporizado e convertido em vapor d’água a . (Ver a Tabela 17.4.) b) Compare sua resposta com a variação de entropia quando de gelo funde-se a , calculada no Exemplo 20.5 (Seção 20.7). A variação de entropia é maior ou menor do que a variação de entropia na liquefação? Interprete sua resposta, usando a ideai de que a entropia esta associada ao grau de desordem de um sistema.
Ver solução completaQuestão 51
Suponha que mols de gás ideal da figura abaixo se expanda até quatro vezes seu volume inicial. Como se vê, as temperaturas iniciais e finais são as mesmas. Calcule a variação de entropia do gás.
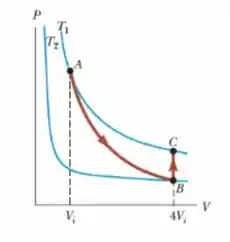
Questão 52
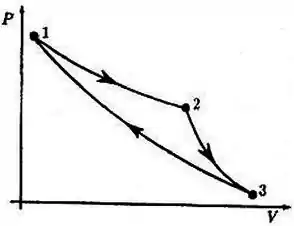
Um engenheiro propôs à sua empresa construir uma máquina térmica onde um gás ideal monoatômico sofre os processos indicados no diagrama da figura:
: processo isotérmico
: processo adiabático
: processo adiabático
A proposta foi rejeitada.
Quais das afirmativas abaixo são justificativas corretas para esta rejeição:
- Esta máquina não funciona pois viola a segunda lei da termodinâmica.
- Esta máquina não interessa pois tem uma eficiência muito baixa.
- O ciclo é inconsistente. Uma das etapas indicadas não pode ocorrer.
- Esta máquina não funciona pois viola a primeira lei da termodinâmica.
- I e III
- I e IV
- I
- IV
- II e IV
Questão 53
Considerando o processo mostrado no diagrama pxV de um gás ideal, qual é a opção correta a respeito do calor trocado nos processos A e B e os valores da entropia nos estados inicial i e final f?
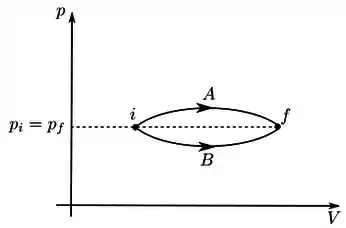
Questão 54
O ciclo da figura abaixo representa a operaçãoo de um motor de combustão interna de gasolina (ciclo de Otto). Suponha que a mistura gasolina-ar é equivalente a mols de um gás ideal com .
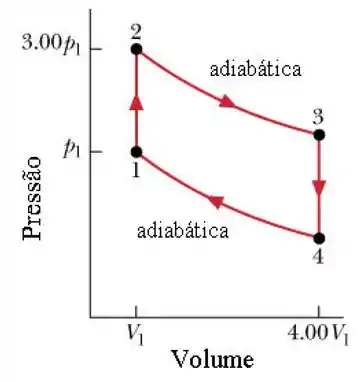
Determine as razões entre as temperaturas absolutas , e .
Determine as razões entre as pressões e .
Determine o trabalho total realizado no ciclo (em função de ).
Em que fase o calor é fornecido ao sistema? Calcule esse calor (em função de ).
Calcule a eficiência dessa máquina, supondo que todas as trocas de calor ocorrem com fontes externas ao sistema.
Determine a variação de entropia da substância de trabalho em cada fase do ciclo (em função de ).
Ver solução completaQuestão 55
Um pequeno objeto de massa , a uma temperatura , é submerso em um reservatório com água a temperatura com Podemos supor que este processo irreversível ocorra a volume constante, sendo o calor específico a volume constante do objeto. Após ter atingido o equilíbrio térmico, a variação da entropia do objeto vale:
Questão 56
Dentro de um calorímetro, uma certa quantidade de água quente, a , é misturada com outra quantidade de água, a temperatura ambiente de . Após algum tempo o sistema atinge o equilíbrio térmico. Seja a variação da entropia da porção de água quente, a variação da entropia da porção de água a temperatura ambiente e a variação da entropia do universo. Podemos afirmar que:
Questão 57
Analise as afirmações abaixo:
I) Todas as máquinas térmicas têm a mesma eficiência.
II) Em todos os processos adiabáticos a entropia diminui.
III) A eficiência de uma máquina térmica que opera no ciclo de Carnot depende apenas da temperatura da fonte mais quente e da temperatura da fonte mais fria.
IV) Todas as máquinas térmicas reversíveis têm a mesma eficiência.
V) Em todos os processos adiabáticos a entropia aumenta ou permanece constante.
VI) Todas as máquinas térmicas que operam no ciclo de Carnot têm uma eficiência teórica de 100%.
São Falsas:
- III e V.
- Apenas I e II.
- Apenas V.
- Apenas V e IV
- I, II, IV e VI
- Apenas I, IV e VI
Questão 58
Marque a afirmativa correta a respeito de uma expansão livre de um gás ideal isolado do ambiente.
(a) A energia interna do gás aumenta e a entropia fica a mesma.
(b) A energia interna e a entropia do gás ficam as mesmas.
(c) A energia interna do gás diminui e a entropia fica a mesma.
(d) A energia interna e a entropia do gás aumentam.
(e) A energia interna do gás fica a mesma e a entropia aumenta.
Ver solução completaQuestão 59
(Cap 20 – Ex 30) Qual é a variação de entropia de do gás hélio no seu ponto de ebulição normal quando todo ele condensa isotermicamente em de hélio líquido? (Sugestão: ver a Tabela 17.4 na seção 17.6.)
Ver solução completaQuestão 60
Considere as seguintes afirmações:
. A variação da pressão de um gás ideal num processo isocórico é proporcional à variação de sua temperatura.
. Em processos isobáricos reversíveis a entropia de um gás ideal varia com o logaritmo da temperatura.
. A energia interna de um gás ideal depende somente de seu volume.
Marque a alternativa CORRETA:
(a) Nenhuma.
(b) Apenas e .
(c) Apenas e .
(d) Apenas .
(e) Apenas e .
(f) Apenas .
Ver solução completaQuestão 61
Suponha que n mols do gás ideal da figura abaixo se expanda até quatro vezes seu volume inicial através do processo indicado na figura abaixo. Como se vê, as temperaturas inicial e final são as mesmas. Calcule a variação da entropia do gás.
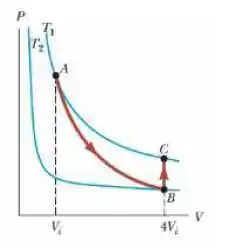
Escolha uma:
Questão 62
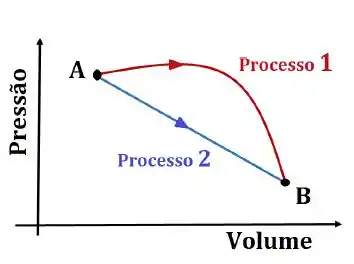
Um gás pode ir do estado ao estado através de dois processos diferentes denotados por “processo1” e “processo 2" na figura ao lado. Compare a variação de energia interna (), o trabalho realizado pelo gás (), o calor recebido pelo gás ( e a variação de entropia () do gás nesses dois processos. Para isso, preencha as lacunas abaixo com uma das quatro opções: (igual); (menor que); (maior que); ou []. Onde o símbolo [] deve ser usado se não houver dados suficientes para fazer uma comparação entre as grandezas em questão nos dois processos.
Questão 63
Suponha que n mols do gás ideal da figura abaixo se expanda até quatro vezes seu volume inicial. Como se vê, as temperaturas inicial e final são as mesmas. Calcule a variação da entropia ΔS do gás.
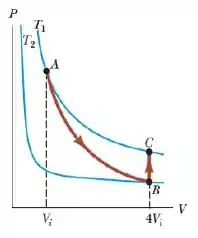
a) ΔS = nRln2;
b) ΔS = nR;
c) ΔS = nR/ln2;
d) ΔS = nR/ln4;
e) ΔS = nRln4;
Ver solução completaQuestão 64
Um gás ideal diatômico () executa uma expansão na qual seu volume dobra de valor . As moléculas do gás podem girar e oscilar (). Determine o valor de , onde é a variação de entropia do gás na expansão e é a constante universal dos gases, nos seguintes casos:
- A pressão do gás cai reversivelmente para a metade .
- O gás se expande livremente, sem absorver calor e sem realizar trabalho.

