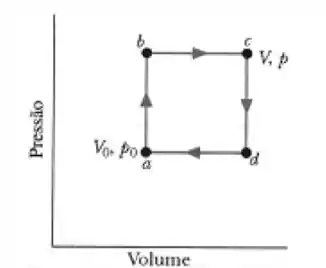
Um mol de um gás ideal monoatômico percorre o ciclo mostrado na figura ao lado. Em c a pressão e o volume são respectivamente e . e são o volume e a pressão em a. Analise as afirmações abaixo:
(I)A temperatura .
(II) A variação da entropia no processo abc é .
(III)A eficiência da máquina que opera com este ciclo é de
(IV). A eficiência de um ciclo de Carnot operando entre as temperaturas mais alta e mais baixa é de .
(V) .
São afimarções verdadeiras:
- Somente III, IV e V
- Somente III e V.
- Somente I e III.
- Todas
- Somente I, III, IV e V.
Passo 1
Vamos analisar uma por uma:
I)
A temperatura em é dada por:
E a de , levando-se em consideração a nova pressão e o novo volume:
E a temperatura em Bom, tem a mesma pressão que e o mesmo volume que
Assim:
A afirmação é falsa.
Passo 2
II)
Temos que:
Vamos analisar primeiro é um processo isovolumétrico, assim:
O valor de é:
A temperatura final é a temperatura em , e a inicial em
O ponto tem a pressão de e o volume de
Assim:
E a variação em vai ser a variação de uma transformação à pressão constante:
Já calculamos essas temperaturas:
Além disso:
Então:
Assim:
Assim, a afirmação é Falsa.
Passo 3
III)
Pra calcular a eficiência, podemos usar:
Pra calcular o trabalho total, devemos calcular os trabalhos dos processos . Além disso, os outros dois processos, são à volume constante, logo, possuem trabalhos nulos.
Assim:
E:
Onde
Assim:
Onde o calor é absorvido? Ele é absorvido nos processos em que ocorre aumento de pressão ou de volume. Assim, em .
O calor absorvido em é:
E o calor absorvido em :
Assim:
Assim:
Assim, a afirmação está correta.
Passo 4
IV)
Pra calcular a eficiência de Carnot, basta aplicar a fórmula:
Quem é É a temperatura mais baixa., assim,
E A temperatura maior. Essa é a que, como vimos, é igual a:
Assim:
Assim: Está correta.
Passo 5
V)
Basta a gente calcular:
E:
Assim, está correta.
Resposta
a)