Exercícios de Retas Paralelas e Perpendiculares - Lista de Exercícios Resolvida

Encontrem quantas retas são normais à curva e paralelas à reta .

Considere a função definida pelo gráfico abaixo, a reta tangente ao gráfico da em e a reta tangente ao gráfico em .

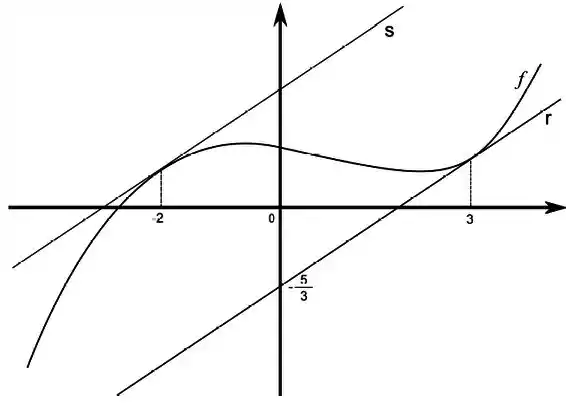
Sabendo , e a reta é paralela à reta , determine:

1. A equação da reta

Calcule a equação da reta tangente à curva no ponto .

A partir da reta tangente, encontre as equações de mais duas retas:

• Reta paralela
• Reta perpendicular

Ambas passando pelo ponto .

Quantas retas tangentes ao gráfico de são paralelas à reta ?

Considere a função definida pelo gráfico abaixo, a reta tangente ao gráfico da em e a reta tangente ao gráfico em .

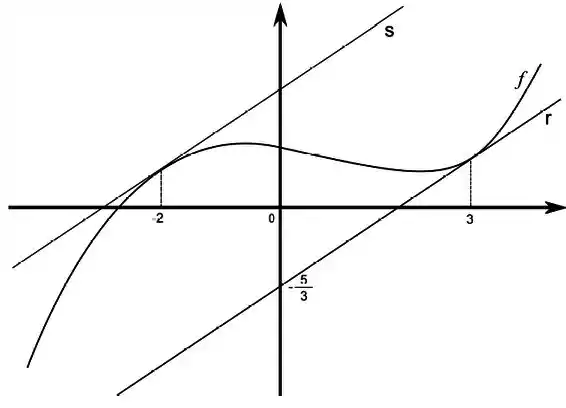
Sabendo , e a reta é paralela a reta , determine:

1. A equação da reta

8 - Determine a equação da reta que é perpendicular à reta e tangente ao gráfico de .

Sejam e constantes e dada por:

Encontre os valores de e para que seja derivável em .

Com os valores de e do item , encontre o ponto do gráfico de onde a reta tangente é paralela à reta .

Em que ponto da curva dada pela equação

A reta tangente é paralela à reta ?

Encontre uma equação para a reta tangente à curva que seja perpendicular à reta .

Determine a(s) reta(s) tangente(s) ao gráfico da função a seguir e perpendicular a reta abaixo

Determine a reta tangente ao gráfico da função a seguir e paralela a reta abaixo

Determine a(s) reta(s) tangente(s) ao gráfico da função a seguir e perpendicular a reta abaixo

4. Determine a reta que é tangente ao gráfico de e paralela à reta .

Encontre as equações das retas tangente e normal à curva:

Nos pontos onde essa curva intersecta a reta

Quantas retas tangentes ao gráfico de são paralelas à reta ? Determine as equações dessas retas.

2) Considere a função cujo gráfico é metade de uma semicircunferência, como esboçado abaixo:

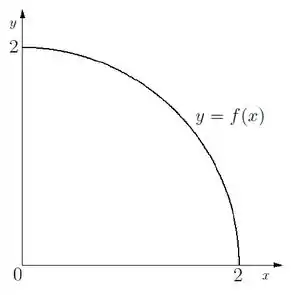
1. Determine a expressão da função
2. Determine a equação da reta tangente ao gráfico de que é paralela .

C9) Refaça o item (c) do exercício C4 com uma função genérica e abscissas genéricas e . Sugestão. Você já fez isso no exercício C3, basta observar que o ponto do gráfico de de abscissa qualquer é .

C4) Considere a função .

d) Determine uma equação para a reta do item (b).

C5) Refaça o exercício anterior para a mesma função e com as abscissas e .

A reta é paralela à reta tangente à elipse no ponto com coordenadas:

1. , .
2. , .
3. , .
4. , .
5. , .

Determine a(s) reta(s) tangente(s) ao gráfico da função a seguir e paralelas a reta abaixo

C4) Considere a função .

a) Faça o gráfico de .

C4) Considere a função .

b) Marque os pontos do gráfico de de abscissas e e desenhe a reta que passa por esses pontos.

Seja definida implicitamente pela equação . Encontre o coeficiente angular da reta normal ao gráfico da função no ponto .

5. Determine uma equação para a reta que passa por e tem coeficiente linear igual a .

C10) Refaça o item (c) do exercício C4 com uma função genérica e abscissas genéricas e .

C4) Considere a função .

c) Determine o coeficiente angular da reta desenhada.

Considere a função abaixo

1. Esboce o gráfico de . (Complete quadrados e use deslocamento e reflexões)

Sabe-se que a reta é tangente ao gráfico de x no ponto e a reta é paralela à reta . Logo a equação da reta passa pelo ponto:

Q03b) Seja dada por

Encontre o ponto do gráfico de onde a reta tangente é paralela à reta

Calcule a derivada de .

Determine os pontos do gráfico de dada no item onde a reta tangente é paralela à reta .

Considere a função , onde .

a) Sabendo que a reta tangente ao gráfico de em é paralela à reta , determine o valor da constante .

b) Atribua à constante o valor encontrado no item anterior. Determine a equação da reta tangente ao gráfico de no ponto de absicissa .

Sendo:

Determine:

1. A reta tangente a essa curva em .
2. Outra reta tangente à essa curva para e paralela a reta do item .

Encontre uma equação da reta tangente à curva que seja paralela à reta .