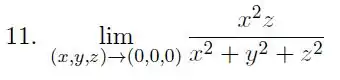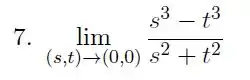Exercícios de Teorema do Sanduíche para Funções de Várias Variáveis - Lista de Exercícios Resolvida

O valor do limite

é

(a) 2.

(b) o limite não existe

(c) 0.

(d)

(e) 1.

Calcule

onde

Seja

Calcule

Sabendo que

você pode dizer algo sobre

Justifique sua resposta.

Calcule ou mostre que o limite não existe.

Calcule , o limite, quando existir. Caso contrário, justifique.

Calcule os seguintes limites, caso existam:

b)

Considere os seguintes limites:

Então:

(a) existe, não existe

(b) existe, existe

(c) não existe, existe

(d) não existe, não existe

(e) nenhuma das outras opções

Calcule , o limite, quando existir. Caso contrário, justifique.

Para cada um dos itens a seguir, mostre se o limite existe ou não. Determine o limite caso exista e justifique suas respostas.

Considere a função

para todo e . O valor do limite é

a) .

b) .

c) .

d) .

e) inexistente.

Seja a função

1. Verifique que

Determine o limite, se existir, ou mostre que o limite não existe (Justifique!)

Calcule, caso exista

Considere os seguintes limites:

Então:

existe e não existe;

existe, existe e são iguais;

existe, existe, mas são diferentes;

não existe e não existe;

não existe e existe.

Calcule, se possível, os limites indicados:

5. Não existe

Calcule o seguinte limite, caso exista:

Determine o limite:

Calcule os seguintes limites abaixo.

Para cada um dos itens a seguir, mostre se o limite existe ou não. Determine o limite caso exista e justifique suas respostas.

Determine o limite, se existir, ou prove que o limite não existe:

Não é permitido usar coordenadas polares.

Calcule os seguintes limites abaixo.

Calcule , o limite, quando existir. Caso contrário, justifique.

Considere a função

para todo e . O valor do limite é

a) .

b) .

c) .

d) .

e) inexistente.

Se

Então

1. não pode ser calculado pois não está definida em
2. não existe

O valor do limite

é

(a) 2.

(b) o limite não existe

(c) 0.

(d)

(e) 1.

Calcule , o limite, quando existir. Caso contrário, justifique.

19. Verifique se é possível utilizar o teorema do confronto para o cálculo dos limites abaixo. Para os casos em que não é possível utilizar o teorema, verifique se o limite não existe.

(b)

19. Verifique se é possível utilizar o teorema do confronto para o cálculo dos limites abaixo. Para os casos em que não é possível utilizar o teorema, verifique se o limite não existe.

(c)

19. Verifique se é possível utilizar o teorema do confronto para o cálculo dos limites abaixo. Para os casos em que não é possível utilizar o teorema, verifique se o limite não existe.

(e)

19. Verifique se é possível utilizar o teorema do confronto para o cálculo dos limites abaixo. Para os casos em que não é possível utilizar o teorema, verifique se o limite não existe.

(f)

19. Verifique se é possível utilizar o teorema do confronto para o cálculo dos limites abaixo. Para os casos em que não é possível utilizar o teorema, verifique se o limite não existe.

(g)

19. Verifique se é possível utilizar o teorema do confronto para o cálculo dos limites abaixo. Para os casos em que não é possível utilizar o teorema, verifique se o limite não existe.

(h)

19. Verifique se é possível utilizar o teorema do confronto para o cálculo dos limites abaixo. Para os casos em que não é possível utilizar o teorema, verifique se o limite não existe.

(i)

19. Verifique se é possível utilizar o teorema do confronto para o cálculo dos limites abaixo. Para os casos em que não é possível utilizar o teorema, verifique se o limite não existe.

(j)

19. Verifique se é possível utilizar o teorema do confronto para o cálculo dos limites abaixo. Para os casos em que não é possível utilizar o teorema, verifique se o limite não existe.

(k)

19. Verifique se é possível utilizar o teorema do confronto para o cálculo dos limites abaixo. Para os casos em que não é possível utilizar o teorema, verifique se o limite não existe.

(l)

19. Verifique se é possível utilizar o teorema do confronto para o cálculo dos limites abaixo. Para os casos em que não é possível utilizar o teorema, verifique se o limite não existe.

(a)

19. Verifique se é possível utilizar o teorema do confronto para o cálculo dos limites abaixo. Para os casos em que não é possível utilizar o teorema, verifique se o limite não existe.

(d)