4) Considere a função , definida para . (Não precisa provar esse fato.)
a) Determine as assíntotas horizontais do gráfico de , ou justifique sua inexistência. Idem, considerando as assíntotas verticais.
b) Determine os intervalos de crescimento e decrescimento da função . Determine ainda os pontos de máximo e de mínimo de (se houver), indicando se são absolutos (globais) ou relativos (locais).
c) Determine os intervalos de concavidade para cima ou para baixo do gráfico de . Determine ainda os pontos de inflexão (se houver).
d) Usando as informações obtidas nos itens anteriores esboce o gráfico de . Deve incluir as assíntotas encontradas, e deve destacar os pontos notáveis obtidos junto com suas coordenadas.
Passo 1
Fala aí, galerinha! Tudo belezinha com vocês?
Bom, a questão deu a função , definida para e pediu uma sequência de coisas pra gente calcular. Se seguirmos procurando cada um dos itens pedidos faremos uma análise bem completa de quem é essa função. Então vamos desenvolver isso juntinhos nos próximos passos. Beleza?
Então esse é o plano. Vem que te mostro como fazer.
Passo 2
a) Na letra a) precisamos determinar, caso seja possível, as assíntotas horizontais, e pra fazermos isso o que precisamos é saber se a função se aproxima de algum valor quando fazemos o ir para ou . Se isso acontecer, nossa função terá uma reta horizontal ao qual ela ficará muito próxima, porém sem nunca tocar.
Um jeito de descobrir isso é calcular o limite da função quando tende a .
Assim,
Porém esses limites não estão definidos no conjunto do números reais, uma vez que teríamos o de um valor negativo.
Essa mesma questão também pede pra gente determinar as assíntotas verticais caso existam, e a ideia aqui é pensar de modo parecido e procura uma reta vertical ao qual a função se aproxima, porém se nunca tocar. Pra gente conseguir fazer isso vamos procurar algum ponto onde a função não esteja definida.
Já temos uma dica do item anterior, já que não podemos calcular o logaritmo natural de um valor menor ou igual a zero. Vamos que a função explode nos valores de que tornam o que está dentro do logaritmo natural menor ou igual a zero.
Veja:
assim,
E
Ou seja, temos duas assíntotas verticais no intervalo dado, uma em e outra em .
Passo 3
b) Na letra b) precisamos determina os intervalos de crescimento e decrescimento da função, e fazemos isso com um estudo de sinal da derivada da função, uma vez que quando a função é crescente sua derivada é positiva e quando a função é decrescente sua derivada é negativa. Assim, faremos:
e
Perceba que o denominador dessa fração é sempre positivo, já que, pelo que vimos no item anterior, . Então a derivada será positiva para valores de (-1,0) e a função será crescente nesse intervalo, já para valores de (0,1) a derivada será negativa e a função será decrescente.
Os pontos críticos acontecem quando a função tem derivada igual a zero, e isso acontecerá para valores de . Como antes desse ponto a derivada da função era positiva e depois dele ela passou a ser negativa, podemos concluir que esse é um ponto de máximo, e será um máximo global já que é o único possível.
Além disso, podemos dizer que a função não possui pontos de mínimo.
Passo 4
c) Para determinar o intervalo de concavidade precisaremos fazer a análise de sinal de . Então vamos derivar novamente a função .
Usando a regra do quociente, termos:
Analisando o sinal, teremos:
Assim, podemos concluir que a concavidade de é voltada para baixo em todo o seu domínio e não existem pontos de inflexão.
Passo 5
Por fim, vamos desenhar o gráfico da função usando as informações que encontramos nos itens anteriores e termos o seguinte resultado:
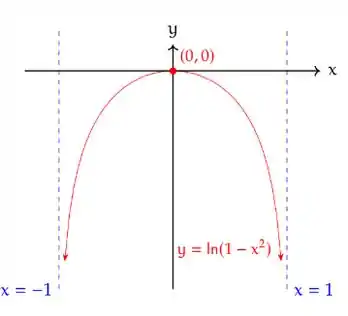
E prontinho! Encontramos nossa resposta!
Resposta
a) Não possui assíntota horizontal. Assíntotas verticais em e .
b) Não possui pontos de mínimo. Máximo global em .
c) Não possui pontos de inflexão. Concavidade voltada para baixo.
d)