UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 4.3.3e
Seja uma função contínua em tal que:
Suponha que o gráfico de seja dada pela figura abaixo:
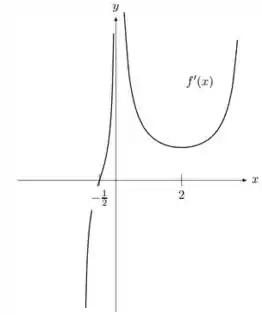
Responde o que se pede:
os pontos de inflexão, caso existam;
Passo 1
Olá gente bonita, tudo bem?
Nessa questão temos uma função , com a informação de algum dos seus pontos:
Também foi dado o gráfico da derivada de , ou seja,
Nesse item precisamos determinar os pontos de inflexão.
Ou seja, são os pontos em que há mudança na concavidade da função. Basicamente, a segunda derivada é nula, ou está em pontos de mudança do sentido do seu crescimento.
No item anterior, determinamos os intervalos em que a concavidade é para cima ou para baixo.
Para determinar os pontos de inflexão, basta vermos os pontos em que houve essa mudança, beleza?
Vamo nessa!
Passo 2
No item anterior, encontramos os seguintes intervalos de concavidade:
Portanto, o ponto em que houve uma mudança da “concavidade para cima” pra “concavidade para baixo” (e vice-versa), foi:
Esse é justamente o pontos de mínimo relativo da derivada de . Ou seja, o pontos em que .
Uma observação importante é que, apesar da concavidade mudar antes e depois de , como esse ponto é uma assíntota vertical para , ele não é considerado um ponto de inflexão.
Prontinho pessoal!
Valeeeu, até mais!