ME02) Considere as afirmações abaixo:
- Se uma função é côncava para cima então ela é necessariamente crescente em todo seu domínio
- O gráfico de uma função pode interceptar o eixo vertical mais de uma vez
Escolha a alternativa correta:
- Ambas são falsas
- Ambas são verdadeiras
- é falsa e é verdadeira
- é verdadeira e é falsa
Passo 1
Bora pelo começo, letra . Está falando de concavidade, mas também fala de crescimento. Uma forma legal de se analisar essa afirmativa é pensar numa pizza dividida entre 4 pessoas:

Pra que isso? Pra dar fome? Não! É pra ajudar mesmo. Vamos repartir os pedaços, ok?
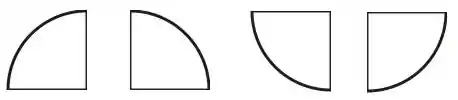
Vamos apagar os raios e adicionar eixos, saca só:
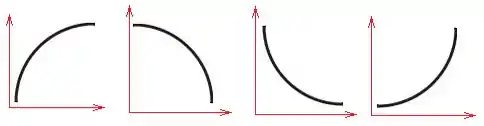
Da esquerda pra direita, temos exemplos de curva:
- Crescente com concavidade pra baixo
- Decrescente com concavidade pra baixo
- Decrescente com concavidade pra cima
- Crescente com concavidade pra cima
O que a letra está nos dizendo é que a curva é impossível. Logo essa afirmativa é falsa!
Passo 2
Vamos continuar pensando na Pizza, mas agora sem tirar os pedaços e só adicionando o eixo:
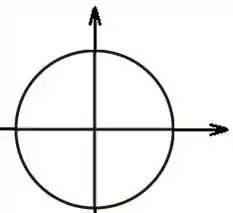
Veja bem, uma circunferência é uma curva que toca o eixo vertical duas vezes, então a deve estar certa. Só um probleminha: uma circunferência não é uma função! Dá uma olhada nesse exemplo:
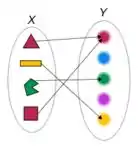
A função acima transforma um objeto na sua cor, por isso da pra dois objetos diferentes terem a mesma cor, mas veja, não da pra um mesmo objeto ter duas cores diferentes! Se uma função tocasse o eixo vertical duas vezes, estaríamos dizendo que isso é possível!
Logo, falso também. Se as duas afirmativas são falsas, a resposta é a letra