Um aparato experimental de fenda dupla é tal que a abertura das fendas é da distância entre elas. Um feixe de luz de comprimento de onda incide sobre as fendas. Em um anteparo, observa-se que o máximo de interferência de 3ª ordem está a uma distância angular de do máximo central.
a) Quantas regiões escuras são observadas dentro da envoltória central de difração? Explique.
b) Qual é a abertura angular da envoltória central de difração?
c) Qual é a intensidade relativa entre o máximo de 4ª ordem e máximo de 2ª ordem?
d) Suponha que a distância entre as fendas é aumentada para o dobro do valor anterior, mantendo o tamanho da abertura de cada fenda. Para cada item (a), (b) e (c) acima, justifique se o novo resultado é igual, maior ou menor ao encontrado anteriormente.
Passo 1
Fala pessoal, prontos para um probleminha sobre difração em fenda dupla?
Bom, você provavelmente já deve ter ouvido falar sobre o experimento de Young em que um feixe de luz passa por duas fendas muito pequenas e os raios interferem criando um padrão de interferência. Esse problema é quase sobre isso, porém aqui vamos considerar também o tamanho das fendas, de modo que o padrão de interferência será um pouquinho diferente.
Vamos chamar de a distância entre as fendas e o tamanho de cada fenda. A expressão para a intensidade no caso com fendas é
onde
Nesse caso, temos , de modo que
Mas sabemos que
Desta forma,
Passo 2
A distribuição da intensidade é mostrada a seguir:
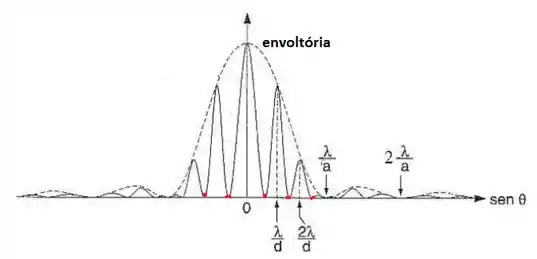
A envoltória é determinada pelos pontos que anulam , enquanto os mínimos dentro da envoltória são determinados pelos pontos que anulam . PS: a figura é totalmente ilustrativa, não leva em conta a relação do problema.
No item (a) queremos saber quantos mínimos de interferência temos dentro da envoltória central. Para isso, vamos achar as posições desses mínimos (pintados de vermelho no desenho)! Nós queremos que
Portanto
Com isso, para , temos que os mínimos de interferência ocorrem em:
Já os mínimos da envoltória ocorrem para
Portanto, esses mínimos acontecem em
Passo 3
Vamos resolver o item (a)! A envoltória central está determinada por
Como , temos que
Mas vimos que os mínimos são dados por , de modo que
Logo,
Com isso, temos
Portanto, existem 9 mínimos secundários dentro da envoltória central!
Passo 4
No item (b) queremos a abertura angular da envoltória central. Essa abertura corresponde a , onde
Já sabemos que , mas ainda não conhecemos . Para achá-lo, vamos usar a seguinte informação “observa-se que o máximo de interferência de 3ª ordem está a uma distância angular de do máximo central”.
Os máximos principais são dados por
Logo,
O máximo de terceira ordem corresponde a :
Como :
Assim, para achar a abertura da envoltória central, usamos
Usando uma calculadora,
Essa é a abertura angular da envoltória central!
Passo 5
No item (c) queremos a intensidade relativa do máximo de ordem com relação ao máximo de ordem . Para isso, vamos usar o resultado que deduzimos no passo 4 para a posição dos máximos de ordem :
Com isso, achamos:
Lembre-se que a intensidade é dada por
É fácil perceber que
Logo, a expressão da intensidade se reduz em apenas
Substituindo o valor de :
Repare que agora estou indicando a intensidade por , que corresponde ao -ésimo máximo de interferência. No caso geral, a relação entre a intensidade do máximo de ordem e o máximo de ordem m será:
Passo 6
Para responder o item (c), devemos usar e :
Vamos usar também que
Assim,
- Logo,
- Com isso, a razão das intensidades será:
Repare que eu fiz toda a conta de forma literal já pensando no item (d), mas isso é assunto para daqui a pouco!
Lembrando que , achamos que
Fazendo a conta em uma calculadora:
Passo 7
Para terminar o problema, vamos para o item (d)! Agora, a distância entre as fendas passa a ser o dobro do que era antes, porém a abertura segue sendo igual. Lembre-se que era , onde é a distância antiga entre as fendas. A distância nova é o dobro da antiga, de modo que se chamarmos essa nova distância de , a abertura deve ser
Se você preferir fazer isso com mais calma, podemos pensar da seguinte forma: antes tínhamos
Agora temos que
Isolando na primeira e substituindo na segunda nós achamos . O problema quer que analisemos as respostas dos três primeiros itens considerando essa mudança...
No item (a) a condição era:
Substituindo :
Isso significa que o número de valores de que satisfaz essa relação vai aumentar. Portanto, a resposta do item (a) aumenta!
Já no item (b), tínhamos que
Usando que , achamos agora
Desta forma,
Esse valor é o dobro do que achamos no item (b). Com isso, a abertura angular será maior!
Por fim, no item (c), vimos que a expressão geral era:
Usando :
Note que esse valor também é maior do que encontramos no item (c). Portanto, o aumento da distância entre as fendas sem modificar a abertura delas aumenta a resposta de todos os itens!
Com isso chegamos ao fim desse problema 😉!
Resposta
9 mínimos secundários dentro da envoltória central.
Aumenta (a), aumenta (a) e aumenta (c).