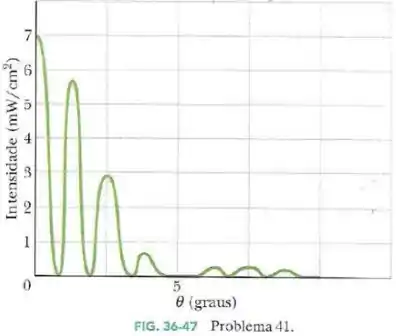
Uma luz com um comprimento de onda de passa por um sistema de dupla fenda e produz uma figura de difração cujo gráfico de intensidade em função da posição angular aparece na Fig. 36-47. Determine:
- A largura das fendas
- A distância entre as fendas.
- Mostre que as intensidades máximas indicadas para as franjas de interferência com e estão corretas.
Passo 1
Letra a)
Pelo gráfico, podemos entender que temos um mínimo de difração em pois os máximos próximos estão achatados e com uma distância bem maior que os outros máximos da figura.
Substituindo nas condições de mínimo de difração:
Onde é a largura da fenda, é o comprimento de onda da luz e , pois este é o primeiro mínimo de difração.
Caso sua calculadora só faça o seno de ângulos em radiano, e você não saiba alterar isso, para converter um ângulo de graus em radianos:
Que é uma regra de três já montada. No nosso caso:
Passo 2
Letra b)
As condições de máximo de interferência são:
Pelo gráfico, a terceira franja clara () corresponde a um ângulo de (duas unidades do eixo horizontal são , logo uma unidade são );
Substituindo essas informações e o comprimento de onda:
Passo 3
Letra c)
A fórmula da intensidade é:
Onde:
Para acharmos a intensidade dos máximos correspondentes a e , nós precisamos primeiro achar seus ângulos. No caso , nos já temos. Substituindo os valores:
Pelo gráfico,
Que bate aproximadamente com o gráfico.
Passo 4
Para , o ângulo é dado por:
Substituindo nas equações:
Substituindo na fórmula de intensidade:
Que também aparece estar de acordo com o gráfico.
Resposta
Letra a)
Letra b)
Letra c)
Como demonstrado, as intensidades máximas do gráfico estão de acordo com as calculadas.