Uma bola de a uma velocidade de atinge uma mola de constante elástica igual a que sofre uma compressão de . Calcule a constante elástica da mola. (Considere )
(a)
(b)
(c)
(d)
(e)
Passo 1
Vamos desenhar o que ele tá falando pra gente, tem uma bola vindo com uma velocidade de e ela comprime uma mola de , aí a gente já transforma pra unidade no SI, então a compressão da mola é :
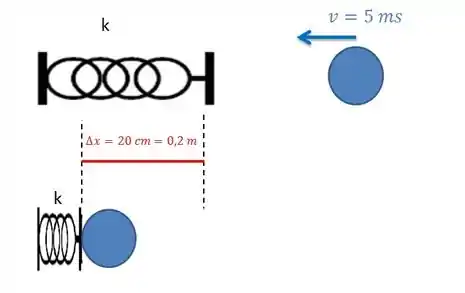
Passo 2
Como não temos forças dissipativas roubando energia do nosso sistema, temos que a energia mecânica do nosso sistema se conserva, então:
No início:
A bolinha tá se movendo, então temos energia cinética.
A mola tá relaxada, então não tem energia potencial elástica.
No final:
A bolinha para, porque ela já comprimiu a mola tudo o quela conseguia.
A mola está comprimida, logo armazena uma energia elástica.
Então:
Arrumando isso:
Substituindo os valores do enunciado (lembrando que as unidades devem estar no SI):
Resolvendo isso daí:
Uhuul! Essa é a resposta!

Resposta
Alternativa A