Exercícios Resolvidos de Energia Cinética + Energia Gravitacional + Energia Elástica
Ver TeoriaEnunciado
Uma pedra de massa e amarrada a um barbante de comprimento é posta para girar em um plano perpendicular ao solo. Em um dado instante ela é solta de forma que, após passar por uma altura máxima, ela vem a atingir uma parede que se encontra a uma distância do ponto de lançamento. A velocidade da pedra no momento do lançamento tem módulo e faz um ângulo com a horizontal. Nestas condições, determine (Todas as respostas devem ser dadas em termos de , , , , e ):
(a) A altura do ponto de impacto da pedra na parede em relação ao ponto de lançamento
(b) a expressão para o vetor velocidade da pedra no momento imediatamente antes dela atingir a parede, em termos dos vetores unitários e indicados na figura
(c) A energia cinética da pedra no instante em que ela passa pelo ponto mais alto de sua trajetória
(d) o módulo da tensão no barbante no momento imediatamente anterior ao lançamento
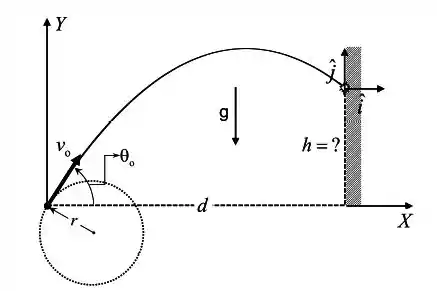
Passo 1
(a)
Temos que no momento do lançamento, a pedra tem uma velocidade que faz um ângulo com a horizontal. Se decompormos essa velocidade nas componentes e , vamos ter
Passo 2
Na direção não há aceleração, logo nessa direção teremos um movimento uniforme
Como e vimos no passo anterior, temos
Enquanto que na direção , como temos a aceleração da gravidade apontando na direção negativa do eixo , teremos um movimento uniformemente variado
Como saímos da origem e ficamos com
Passo 3
Quando a pedra bate na parede temos que as suas posições e são dadas por
Lembrando que queremos encontra a altura ! Isolando na primeira equação, temos
Agora basta substituir na segunda equação
Dando uma trabalhada pra essa expressão ficar mais simpática, ficamos com
Passo 4
(b)
Pra encontrar esse vetor , temos que achar as suas componentes
Basta usar as equações da posição que já tínhamos
De forma que as componentes e são dadas por
Como no momento em que a pedra toca a parede o tempo vale (vimos lá no passo 3)
Basta substituir
Assim o nosso vetor vai ser dado por
Passo 5
(c)
No ponto mais alto da trajetória temos que a velocidade na direção é nula. Assim o nosso vetor velocidade vai ser dado por
Já que a velocidade na direção vai ser sempre a mesma (movimento uniforme)
E a intensidade da velocidade será dada por
Passo 6
A energia cinética vai ser dada por
Passo 7
(d)
Antes da pedra ser lançada ela está em uma trajetória circular. O que isso te lembra? Força centrípeta, né? Como logo antes do lançamento ela tem uma velocidade , então a força centrípeta é dada por
Passo 8
Agora para achar a tensão na corda temos que fazer o diagrama de corpo livre pra essa pedra. No caso, sobre ela teremos a tração e o seu peso
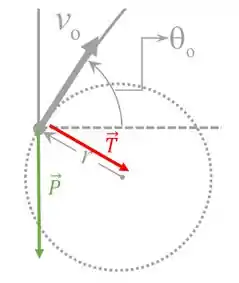
Passo 9
A tração já tá no esquema apontando pro centro da trajetória. Já o peso nem aponta na direção tangencial e nem aponta na direção radial. Pra trabalhar com ele teremos que decompor o peso nessas duas direções! Tá vendo esse ângulo ?! Ele vai ser o cara na nossa decomposição! Saca só
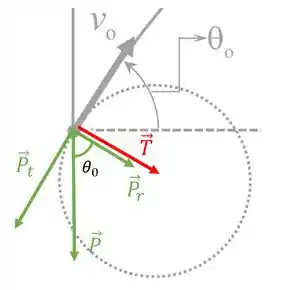
Pela nossa figura a componente do peso que aponta na direção radial é dada por
Passo 10
Como a tensão e essa componente radial apontam pro centro da curva a força centrípeta será dada por
Substituindo o que achamos antes
Resposta
(a)
(b)
(c)
(d)