Se a posição de uma partícula é dada por , onde está em metros e em segundos, em que instantes a velocidade da partícula é zero? Em que instantessa aceleração é zero? Para que intervalo de tempo positivo e negativo a aceleração é negativa? Para que intervalo de tempo positivo ou negativoa aceleração é positiva? Trace os gráficos de .
Passo 1
Essa é uma questão com vários itens mas não precisa entrar em desespero, tudo partirá da equação da posição e usaremos bastante as derivadas por aqui, beleza? Vem comigo que eu te mostro o passo a passo.
Para descobrir o instante em que a velocidade é zero, primeiro precisamos descobrir a equação da velocidade. Para encontrarmos a equação da velocidade é só a gente derivar a equação da posição.
Passo 2
Então para descobrir o tempo pra qual a velocidade é zero vamos zerar a velocidade
Ou seja, a velocidade será zero nos tempos e .
Passo 3
Para descobrir os instantes que a aceleração é zero, devemos achar a equação da aceleração, ela é a derivada da velocidade se liga aí:
Passo 4
De novo queremos o tempo quando a aceleração é zero, então faremos .
Passo 5
Aceleração é negativa quando
Se tratando de uma função linear não tem muito mistério, vamos substituir e analisar o que rola.
Dividindo os dois lados por , temos isolado e a relação fica:
Para tempos maiores que a aceleração é negativa.
Se liga, que inverteu-se o sinal da inequação ali em cima!Isso acontece, por que dividimos por um número negativo dos dois lado da inequação
(E sempre que multiplicarmos ou dividirmos uma inequação por um número negativo, é necessário inverter o sinal da inequação!)
Passo 6
Para a aceleração ser positiva
Seguindo a mesma idéia usada no item As acelerações positivas vão ocorrer para os seguintes tempos.
Ou seja, para tempo menor do que zero, a aceleração será positiva.
Passo 7
Para traçar o gráfico pegaremos os pontos de máximo e mínimo fazendo a derivada da função igual a zero que nesse caso, pasmem é a velocidade que já calculamos pra esse ponto.
Para , encontramos os seguintes valores de lá no passo
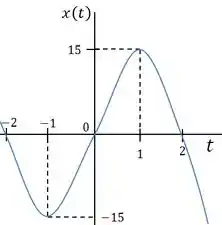
Voltando com esses valores de para a equação da posição temos os valores de máximo e mínimo, começando com o valor positivo.
Para o valor negativo temos:
Um outro ponto relevante é a origem e nesse caso podemos substituir .
Podemos então plotar o gráfico com esse comportamento.
Passo 8
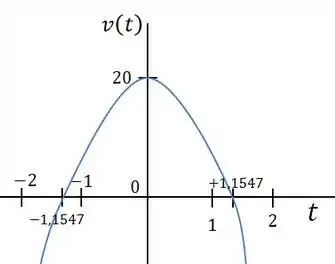
Para fazer o gráfico de vamos analisar a equação da velocidade, que é um polinômio de segundo grau
Calculamos que essa parábola corta o eixo nos pontos , onde avaliamos qual era o tempo de .
Para encontrar o ponto de máximo, basta derivar a equação e igualar a zero. Mas se liga a gente já fez isso, lembra que a derivada da velocidade é a aceleração?
A gente também avaliou o ponto onde e concluímos que é quando , agora vamos pegar esse tempo e substituir na eq. da velocidade.
Agora é só plotar o gráfico e correr pro abraço:
Passo 9
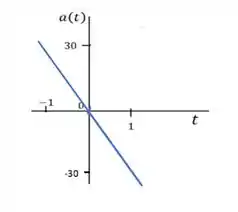
A equação da aceleração a gente calculou e é essa aqui:
Descreve uma reta com inclinação negativa. Nós também avaliamos que a aceleração tem valor na origem para e portanto temos o seguinte gráfico.
Resposta