A posição de uma partícula que se move ao longo do eixo é dada em centímetros por , onde está em segundos. Calcule a velocidade média durante o intervalo de tempo de a a velocidade instantânea em a velocidade instantânea em a velocidade instantânea em a velocidade instantânea quando a partícula está na metade da distância entre suas posições em e Plote o gráfico de em função de e indique suas respostas graficamente.
Passo 1
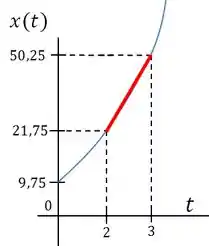
Velocidade média é dada pela fórmula
Para calcularmos devemos achar as posições nos instantes e
Passo 2
Podemos aplicar a equação da velocidade média
Passo 3
Para calcularmos a velocidade instantânea devemos achar a função velocidade e para isso vamos derivar a função posição
A velocidade instantânea no instante é dada por
Passo 4
Vamos substituir por para descobrirmos a velocidade nesse instante
Passo 5
Faremos o mesmo para
Passo 6
O primeiro passo é descobrir em que instante a partícula está na metade da distância entre os instantes e
No item calculamos
Assim a metade entre essas posições é
Passo 7
Descobrimos a posição que equivale a metade do caminho entre e , agora conseguimos descobrir em que instante isso acontece
Passo 8
Agora é só substituir esse valor de na função velocidade para descobrirmos qual era a velocidade naquele instante
Passo 9
Como a função da posição é um polinômio de grau e vamos considerar podemos prever que o gráfico crescerá infinitamente començando em
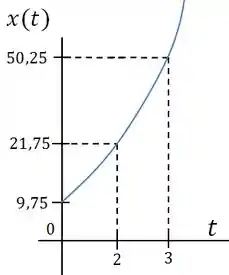
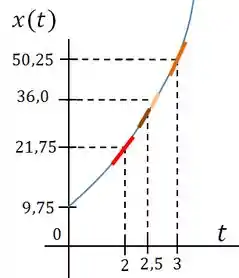
Passo 10
A resposta do item seria obtida fazendo a tangente da reta em vermelho
Passo 11
E as respostas nos demais itens seria obtida fazendo a tangente dos pontos respectivos a seus instantes ou posição
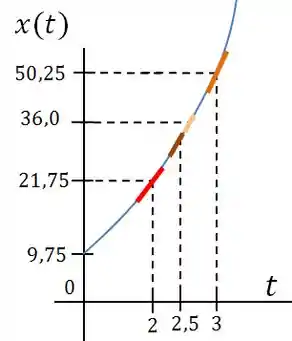
Resposta
a)
b)
c)
d)
e)
f)