Física 2 - UFF; P1 de 2019.2
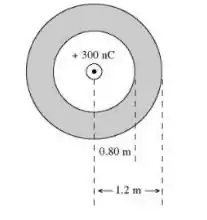
6 - Uma esfera condutora oca tem raios de e , como mostrado na figura. A esfera carrega um excesso de carga . Uma carga pontual de está presente no centro da cavidade interna à esfera. A densidade de carga superficial na superfície esférica interna vale
- Zero
Passo 1
Ora, se temos uma carga de no interior da esfera oca, isso vai fazer com que apareça na superfície interna da esfera oca.
Como área interna da esfera é:
Então a densidade de carga pode ser calculada assim:
Lembre-se de que é nano e vale
Resposta
Letra D.
Exercícios de Livros Relacionados
Uma fina casca esférica não condutora, uniformemente carregada, com raio R , tem uma carga total positiva igual a Q ; Um pequeno pedaço é removido da superfície. (a) Quais são o módulo, a direção e o
Duas placas metálicas quadradas idênticas têm, cada uma, área de 500c m 2 . Elas são separadas por 1,50c m e estão, ambas, inicialmente descarregadas. A seguir, uma carga de + 1,50n C é transferida da
Uma lâmina plana infinita não condutora tem uma densidade superficial de carga + 3,00μ C / m 2 e está no plano y = - 0,600m . Uma segunda lâmina plana infinita tem densidade superficial de carga de -
O pequeno segmento de fio na FIGURA Q27.4 contém 10n C de carga. a. O segmento é reduzido a um terço do comprimento original. Qual é a razão λ f / λ i , onde λ i e λ f são as densidades de carga inici
Um disco circular está carregado e sua uma densidade superficial de carga vale 8n C / c m ² ² . Qual será a densidade superficial de carga se o raio do disco for dobrado?