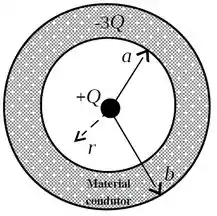
A figura ao lado ilustra uma esfera oca condutora de raio interno e raio externo , que tem uma carga elétrica negativa . Uma carga pontual positiva é fixada no centro da esfera oca. Na figura, representa uma distância radial qualquer ao centro da esfera. Existe vácuo nas regiões e .
(a) Calcule o vetor campo elétrico (módulo, direção e sentido) em todos os pontos do espaço, ou seja, nas regiões (i) , (ii) e (iii) .
(b) Represente, em um desenho esquemático, um esboço das linhas de campo elétrico nas regiões , e .
(c) Determine a densidade superficial de carga na (i) superfície interna da esfera oca () e na (ii) superfície externa da esfera oca ().
Passo 1
Aqui, estamos interessados apenas no item (c).
Então, a densidade superficial de carga nada mais que é a quantidade de carga por unidade de área, certo?
Temos que lembrar aqui que a área de uma superfície esférica é dada por:
Sendo o raio da superfície esférica.
Também temos que lembrar aqui, que a casca esférica é condutora, portanto, na sua superfície interna teremos a carga , que foi atraída para essa superfície por conta do efeito de indução eletrostática.
E para a carga na superfície externa, teremos a carga , pois a carga total na casca esférica é , e como já foi para a superfície interna, resta para a superfície externa.
Passo 2
Assim sendo, para cada uma das regiões (i) superfície interna da esfera ( e (ii) superfície externa da esfera (), temos:
ii.
Resposta
As densidades superficiais de carga para as regiões (i) e (ii) são dadas, respectivamente, por:
- ; e