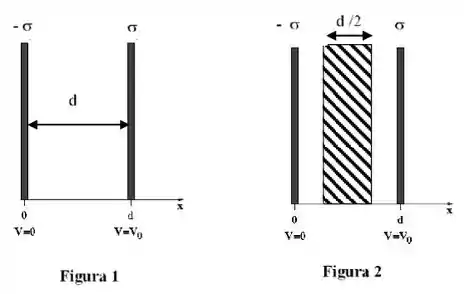
Duas placas isolantes muito grandes e de espessura desprezível são colocadas paralelamente uma em relação a outra, como mostrado na Figura 1. Na placa à direita, há uma distribuição superficial uniforme de cargas positiva. Na placa à esquerda, a distribuição de cargas é também uniforme, porém de densidade superficial igual e oposta à da direita. A distância entre as placas vale d e existe o vácuo entre as duas. Tomando a placa à esquerda (na posição ) como o referencial para o potencial mede-se que, sobre a placa à direita , o potencial tem valor.
a) Calcule a densidade superficial de cargas, , da placa isolante positiva em função de .
b) O sinal de é positivo ou negativo? Justifique.
Suponha agora que uma placa condutora neutra de espessura seja colocada na região entre as duas placas isolantes, como mostrado na Figura 2. Nesta nova configuração:
c) Calcule os valores do potencial em e faça um gráfico do potencial em função da distância para .
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Letra (a):
Vamos começar calculando o campo elétrico.
O campo elétrico devido a uma placa isolante infinita é:
Para temos:
E agora podemos através da definição integral de potencial, achar :
Sabemos que , então:
E agora por fim, isolamos :
Passo 2
Letra (b):
Como por definição no problema, . E, claramente o potencial cai à medida que se afasta da placa positiva, e consequentemente aumenta ao se aproximar da negativa.
Como , .
Tranquilo? Vamos para o último item?
Passo 3
Letra (c):
Dentro da placa condutora, . Assim o condutor distribui suas cargas para cumprir essa condição. Na região entre as placas o potencial cresce linearmente. Na região dentro do condutor o potencial é constante.
Dentro:
Fora:
Então é:
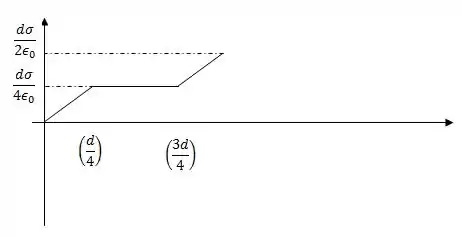
E em um gráfico fica assim:
Beleza?
Pronto pra próxima questão? =)
Resposta
Como , .