Um átomo de hidrogênio é constituído por um próton com carga e um elétron com carga . Podemos considerar o próton como uma carga puntiforme situada em , o centro do átomo. O movimento do elétron faz com que sua carga seja ‘espalhada’ ao longo de uma distribuição esférica em torno do próton, de modo que o elétron seja equivalente a uma carga por unidade de volume dada por
em que é chamado de raio de Bohr.
- Calcule a carga total do átomo de hidrogênio contida em uma esfera de raio centralizada sobre o próton;
- Como fica a carga quando ? Explique o resultado obtido nesse limite.
Passo 1
Neste exercício, temos basicamente o que está representado na Figura a) abaixo. O próton, com carga positiva localizado na origem e a carga do elétron distribuída ao longo de uma esfera de raio com uma densidade de cargas com comportamento exponencial.
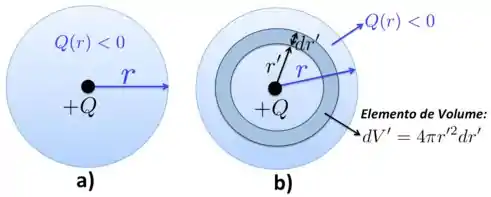
A carga total da Figura a) é dada por
sendo que é a carga ‘espalhada’ do elétron dentro da esfera de raio , que é negativa. Para obtermos a carga total, primeiro vamos calcular a carga do elétron...
Passo 2
a) Para calcularmos , vamos utilizar a Figura b), que mostra um volume ’. Incluindo esse elemento de volume e a densidade volumétrica dada, temos que a carga total é dada por
Como você faz lá no cálculo frequentemente, poderíamos utilizar a integral por partes duas vezes na integral acima e obter o resultado. Aqui, para a gente avançar mais rápido, vou te mostrar o resultado de integrais desse tipo:
em que é uma constante de integração. Aplicando esse resultado em e substituindo os limites de integração, você vai chegar no seguinte:
Somando esse resultando com a carga do próton, a carga total será
Podemos simplicar um pouco mais para obter que:
Passo 3
b) No limite de , como a função exponencial vai a zero mais rapidamente do que as funções de dentro dos parênteses vão para infinito, então, teremos que:
Esse é um resultado esperado, pois se a gente integra sobre todo o espaço, carga total será
que é exatamente a soma das cargas do próton e do elétron, fazendo com que o átomo de hidrogênio seja neutro.
Resposta
- pois o átomo de hidrogênio como um todo é neutro.