Um disco de raio de espessura desprezível tem um furo circular em seu centro. Dado que o raio do furo é e o disco possui densidade de carga superficial igual a:
Com tendo unidades de carga. Calcule a carga total do disco.
Passo 1
Desenhando o que foi descrito temos:
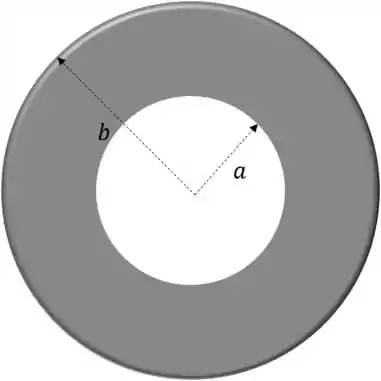
Passo 2
Como queremos a carga total, utilizamos a definição da densidade superficial:
E trocamos o diferencial de área por sua expressão em coordenadas polares. Uma dica para os impacientes (tipo eu): calcule o diferencial com calma. A expressão para a área do círculo você conhece:
Derivando:
E assim evitamos erros crassos, como o que eu acabei de cometer resolvendo essa questão haha.
Passo 3
Integrando em todo o disco:
Segue que:
Puxando o pra fora e arrumando:
Finalmente fazemos a conta da integral:
Arrumando novamente: