Densidade de Carga
Um anel circular, fino, de raio , está disposto no plano , com centro na origem. Nele, há uma densidade linear de carga , onde é o tradicional ângulo polar e é uma constante. Qual é a carga total de tal anel?
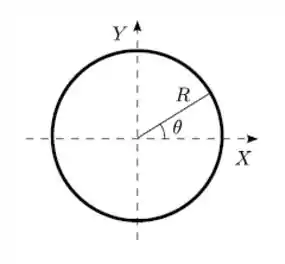
- 0
Passo 1
Achara a carga total é igual à integrar a densidade em todo o corpo:
Passo 2
Utilizando coordenadas polares e substituindo os valores das paradas:
Em coordenadas polares:
Passo 3
Como a densidade linear de carga depende do módulo do seno do ângulo, devemos separar a integral em duas, pois para 0, e para . Separando a integral:
Resolvendo a bandida:
Tomando cuidado pra não se ferrar com os sinais:
Resposta
Letra e
Exercícios de Livros Relacionados
Uma fina casca esférica não condutora, uniformemente carregada, com raio R , tem uma carga total positiva igual a Q ; Um pequeno pedaço é removido da superfície. (a) Quais são o módulo, a direção e o
Duas placas metálicas quadradas idênticas têm, cada uma, área de 500c m 2 . Elas são separadas por 1,50c m e estão, ambas, inicialmente descarregadas. A seguir, uma carga de + 1,50n C é transferida da
Uma lâmina plana infinita não condutora tem uma densidade superficial de carga + 3,00μ C / m 2 e está no plano y = - 0,600m . Uma segunda lâmina plana infinita tem densidade superficial de carga de -
O pequeno segmento de fio na FIGURA Q27.4 contém 10n C de carga. a. O segmento é reduzido a um terço do comprimento original. Qual é a razão λ f / λ i , onde λ i e λ f são as densidades de carga inici
Um disco circular está carregado e sua uma densidade superficial de carga vale 8n C / c m ² ² . Qual será a densidade superficial de carga se o raio do disco for dobrado?