Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Densidade de Cargas

Ver Teoria
Exercício 2412345678910111213141516171819202122232526272829

Enunciado

PUCRIO – Física 3 2020.1 – G1– Questão 8

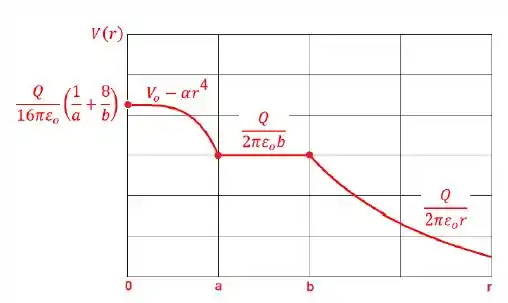
Um isolante esférico de raio a tem carga total Q (positiva) e está envolvido por uma casca esférica concêntrica de raios   a e b , condutora em equilíbrio eletrostático. Não se sabe se a distribuição da carga no interior do isolante é uniforme ou não. A estrutura está imersa no vácuo (para r   >   b ) . O potencial elétrico em todos os pontos do espaço ( r   >   0 ) está caracterizado na Figura. Em particular, observam-se as dependências de V(r) com o raio r nos intervalos 0   <   r   <   a   [ V ( r )   =   V o   - α r 4 ] ; a   <   r   <   b ;   r   >   b e que V 0   =   V ( 0 ) .

a) Após determinar o valor de  em função de Q, a, b e ε o (considerando que o potencial é uma função contínua de r , obtenha expressões para o campo elétrico em todos os pontos do espaço).

b) Em seguida, determine as distribuições superficiais de carga (com sinais) nas superfícies interna (raio a ) e externa (raio b) da casca condutora. Calcule a carga líquida da casca condutora, se houver.

Passo 1

Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?

Letra (a):

Da figura temos que em r = a :

V 0 - α a 4 = V a = Q 2 π ϵ 0 b

α a 4 = V 0 - Q 2 π ϵ 0 b

α = 1 a 4 V 0 - Q 2 π ϵ 0 b = Q 16 π ϵ 0 1 a 5

O campo elétrico é:

E → = - d V d r r ^

Para r < a :

E → r = Q 4 π ϵ 0 1 a 2   r a 3 r ^

Para a < r < b :

E → = 0

Para r > b :

E → r = 2 Q 4 π ϵ 0 1 r 2 r ^

Passo 2

Letra (b):

Observa-se que os vetores unitários normais à superfície interna e ( r = a ) externa ( r = b ) da casca condutora são n ^ a = - r ^ e n ^ b = r ^ .

Combinando estes vetores unitários com o resultado do item anterior e com a expressão geral:

σ s u p = ϵ 0 E → s u p ⋅ n → s u p

Temos:

σ a = ϵ 0 Q 4 π ϵ 0 1 a 2 a a 3 r ^ ⋅ - r ^ = - Q 4 π a 2

E:

σ b = ϵ 0 2 Q 4 π ϵ 0 1 b 2   r ^ ⋅ r ^ = 2 Q 4 π b 2

E a carga líquida da casca esférica é:

Q l i q = 4 π b 2 σ b - 4 π a 2 σ a

Q l i q = 2 Q - Q = Q

Beleza?

Pronto pra próxima questão? =)

Resposta

a )   Para r < a :

E → r = Q 4 π ϵ 0 1 a 2   r a 3 r ^

Para a < r < b :

E → = 0

Para r > b :

E → r = 2 Q 4 π ϵ 0 1 r 2 r ^

b ) Q l i q = Q

Exercícios de Livros Relacionados

Uma fina casca esférica não condutora, uniformemente carregada, com raio R , tem uma carga total positiva igual a Q ; Um pequeno pedaço é removido da superfície. (a) Quais são o módulo, a direção e o
Duas placas metálicas quadradas idênticas têm, cada uma, área de 500c m 2 . Elas são separadas por 1,50c m e estão, ambas, inicialmente descarregadas. A seguir, uma carga de + 1,50n C é transferida da
Uma lâmina plana infinita não condutora tem uma densidade superficial de carga + 3,00μ C / m 2 e está no plano y = - 0,600m . Uma segunda lâmina plana infinita tem densidade superficial de carga de -
O pequeno segmento de fio na FIGURA Q27.4 contém 10n C de carga. a. O segmento é reduzido a um terço do comprimento original. Qual é a razão λ f / λ i , onde λ i e λ f são as densidades de carga inici
Um disco circular está carregado e sua uma densidade superficial de carga vale 8n C / c m ² ² . Qual será a densidade superficial de carga se o raio do disco for dobrado?