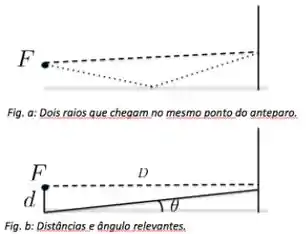
A figura abaixo ilustra o funcionamento de um espelho de Lloyd.
Luz emitida por uma fonte puntiforme pode atingir o anteparo diretamente ou então através de uma reflexão no espelho horizontal, provocando um padrão de interferência no anteparo. Dois destes raios (um pontilhado e outro tracejado) estão indicados na figura .
Seja a distância entre a fonte e o plano do espelho, a distância entre a fonte e o anteparo () e o ângulo de observação, conforme ilustrado na figura .
Sabendo que ao refletir no espelho a onda luminosa ganha uma fase de , assinale a alternativa que está INCORRETA.
- O padrão de interferência produzido é equivalente a termos duas fontes emitindo coerentemente e defasadas por , com a segunda fonte estando na posição da imagem da primeira, com relação ao espelho plano.
- O espaçamento entre os máximos e mínimos consecutivos na interferência é dado por .
- Uma região com interferência destrutiva no anteparo se dá em .
- A intensidade máxima no anteparo é quatro vezes maior do que a intensidade emitida pela fonte .
- A intensidade média ao longo de um período de oscilação é , onde é intensidade emitida por .
Passo 1
Narrando a história de resolver essa questão:
“MEU CRISTO!!! Daonde eles tiram essas coisas? Como drogas vou resolver isso? Olha essas opções... ‘espaçamento’, ‘região bla bla’, ‘o padrão produzido é equivalente’, ‘a intensidade’, como eu vou resolver isso????”
Então, ele lê as opções novamente, e denovo, e denovo, e denovo, até que....
Vem aquela epifania divina. “Olha, eu não sei resolver isso. Mas isso é engraçado, um espelho né, é como se ele espelhasse tudo....”

E aí você lê novamente a letra .
“O padrão de interferência produzido é equivalente a termos duas fontes emitindo coerentemente e defasadas por , com a segunda fonte estando na posição da imagem da primeira, com relação ao espelho plano.”
E agora eu te digo: essa opção está CORRETA!
Todos os raios que vêm da fonte , refletem no espelho e vão pro anteparo, geometricamente é equivalente a se o raio saísse de um ponto , que é o reflexo da fonte.

Porém, em relação à diferença de fase, o raio espelhado sofreu uma diferença de fase de .
Assim, o que temos é um problema que sabemos resolver: Duas fontes pontuais, com uma distância ( está a uma distância do espelho, e sua imagem também, somando dá ) entre elas. Isso é interferência por duas fendas pontuais!
Mas com um plot twist de que elas já começam defasadas por .
Passo 2
Agora podemos avaliar o resto. Para saber se a letra está correta, precisamos avaliar onde ficariam as franjas de mínimo de interferência. Então, lá vamos nós avaliar diferença de fase.
Em relação ao caminho, o que temos é duas “fendas pontuais” com distância , logo:
Porém, tem a diferença de fase por causa da reflexão, que é .
Logo, a diferença de fase total é:
Os mínimos vão ser dados por:
Igualando, teremos interferência destrutiva para:
(eu pulei algumas etapas de algebrismo, espero que possam me perdoar)
Na aproximação de pequenos ângulos, de fato teremos para mínimos consecutivos:
Porém, a aproximação de pequenos ângulos só é válida pra , onde o erro é menor que , acima disso ela começa a falhar miseravelmente (e você será zoado pelos alunos de matemática).
Assim, para pontos próximos do centro do anteparo, isso estaria correto. Mas a afirmação dele é geral, para todos os pontos do anteparo. Isso sim está errado.
Então essa é nossa opção incorreta, letra . Mas vejamos o resto.
Passo 3
A letra diz que “uma região com interferência destrutiva no anteparo se dá em ”.
Bem, para , , e não temos mais diferença de fase por diferença de caminho. Só sobra a diferença de fase por reflexão.
Em termos de comprimento de onda, essa diferença de fase é de meio comprimento de onda. Isso significa que ela é destrutiva.
Assim, de fato no centro da imagem teremos um mínimo de interferência, e essa letra está correta.
Passo 4
As duas últimas vou colocar no mesmo bolo (de nozes).
Letra diz que “a intensidade máxima no anteparo é quatro vezes maior do que a intensidade emitida pela fonte ”.
Letra diz que “a intensidade média ao longo de um período de oscilação é , onde é intensidade emitida por ”.
Como ainda estamos tratando de interferência por duas fendas pontuais, o formato da intensidade no anteparo continua parecido, com oscilações bonitinhas (embora agora, o meio seja de interferência destrutiva).
Isso significa que ainda vale que a intensidade máxima é quatro vezes maior do que a intensidade emitida .
Então a letra está correta. De fato, o formato da intensidade ainda vai ser:
O que muda agora é o termo , que é a diferença de fase entre as fontes (porque ele agora tem um termo somado).
Sendo assim, em um período de oscilação, a gente vai de um mínimo com até outro mínimo, com , passando por um máximo .
Como é uma função que cresce igual ela descresce, tem um resultado que diz que a sua média ao longo de uma oscilação é igual a metade do seu valor máximo. Logo:
Ou seja, a letra também está correta.
Observação:
Eu sei, eu carteei essa média do coseno ao quadrado. Mas acontece que a média dele, ao longo de uma oscilação, seria:
Essa integral vai dar , e aí voce fica com os . O motivo disso dar certinho é, de fato, o que eu falei antes. Como um desenho diz mais que mil palavras:
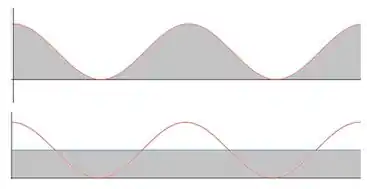
A parte de cima dos morrinhos (em branco na segunda imagem) vão ser iguais ao laguinho que fica nos vales (a parte que era branca na imagem de cima, mas fica cinza na de baixo, embaixo do traço reto que representa a metade da altura).
Resposta
Letra
O espaçamento entre os máximos e mínimos consecutivos na interferência é dado por .