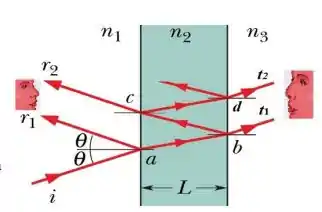
A figura ao lado mostra uma onda incidente quase normal à superfície de um filme fino (índice de refração ) suspenso no ar ( = = ) onde > . A onda é a refletida na primeira superfície em a. A onda é a refletida em b (dentro do filme) e transmitida de volta para o ar na primeira superfície em c. As ondas transmitidas que atravessam o filme são dadas por e . Considere L a espessura do filme e λ o comprimento de onda da luz no filme. Os observadores estão representados pelos rostos desenhados. Ocorre interferência construtiva:
1-( ) se L = para observador que vê as ondas e .
2-( ) se L = para observador que vê as ondas e .
3-( ) se L = para observador que vê os ondas transmitidas e .
4-( ) se L = para observador que vê os ondas transmitidas e .
Passo 1
Nesse caso devemos lembrar como funciona o esquema de interferência em filmes finos.
Sabemos que temos 2 formas de termos interferência que são destrutiva e construtiva.
Sabemos também existem duas formas de termos diferenças de fase, uma por caminho percorrido, e outra quando temos uma reflexão de um meio menos refringente para uma mais refringente, somente nesse caso ocorre mudança de fase.
No nosso caso isso ocorrerá, somente, na passagem do ar para o vidro.
Vamos chamar de fase 1 e a mudança de fase chamaremos de , analisando dessa forma teremos a figura a seguir
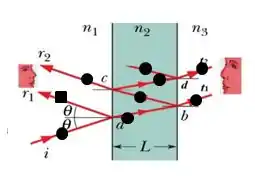
Com isso percebemos que entre e existe uma diferença de fase por reflexão de
E entre os raios e uma diferença de fase por reflexão de
Passo 2
Agora vamos analisar a diferença de fase por caminho percorrido. Sabemos que a fórmula geral é
Teremos que entre os raiose a diferença de fase por caminho percorrido é
Para os raios e temos que a diferença de fase por caminho percorrido também é
Passo 3
Beleza , mas o nosso objetivo é que a interferência entre as ondas seja construtiva, ou seja, elas devem ser múltiplas de 2π, então teremos.
Passo 4
Entre e
Fazendo m=0
Passo 5
e
Para m=1
Passo 6
Analisando as opções vemos que a única que atende as exigências de diferença de fase, interferência construtiva e formula final da espessura é a ultima opção, todas as outras fórmulas finais são incoerentes com as achadas.
Resposta
4-( v) se L = para observador que vê os ondas transmitidas e .