Um filme fino de um certo líquido é mantido em um disco horizontal, com ar dos dois lados do filme. Um feixe de luz com um comprimento de onda de incide perpendicularmente ao filme, e a intensidade da reflexão é medida.
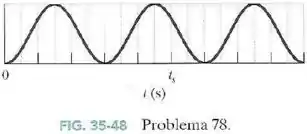
A Fig.35-48 mostra a intensidade em função do tempo ; a escala do eixo horizontal é definida por . A intensidade muda por causa da evaporação nas duas superfícies do filme.
Suponha que o filme é plano, que as duas superfícies do filme são paralelas e que o filme tem um raio de e um índice de refração de . Suponha também que o volume do filme diminui a uma taxa constante.
Determine essa taxa.
Passo 1
Primeiramente, vamos colocar a taxa da variação do volume em termos que saibamos calcular.
Como o volume é igual a área da base multiplicado pela altura, temos:
Onde a altura do filme é na verdade a espessura do mesmo. Como a taxa de variação do volume é constante, podemos substituir nossas derivadas:
Passo 2
Agora precisamos de uma variação de espessura cujo tempo de variação nós saibamos.
De fato, tem uma variação que sabemos calcular: a variação de espessura entre um mínimo de intensidade e outro, correspondendo a interferência destrutiva.
A condição de interferência destrutiva é dada por:
A altura é dada por:
Como o líquido está evaporando, a altura está diminuindo. Isso significa que estamos indo de um mínimo de ordem para um de ordem . A nova altura será:
Passo 3
Ok, temos a variação de espessura entre dois mínimos, mas quanto tempo leva essa variação?
O gráfico tem uma escala de pra cada unidade do eixo do tempo. Assim, o tempo entre dois mínimos é de .
Passo 4
A taxa de variação da altura vai ser:
Passo 5
Pra chegarmos na variação do volume, ainda precisamos da área do disco.
A área da base do disco é dada por , sendo que .
O nosso disco tem então uma área de
Passo 6
Agora sim, podemos encontrar a taxa de variação do volume. Juntando os dois cálculos anteriores:
Resposta
A taxa de variação do volume é de .