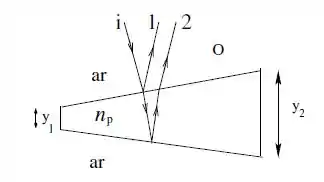
A figura abaixo mostra um bloco de plástico transparente com índice de refração e espessura que varia continuamente entre (extremidade esquerda) e valor (extremidade direita). Um feixe de luz monocromática de comprimento de onda incide normalmente sobre toda a extensão do bloco e é refletida na direção do observador O. Ele observa o bloco numa visão superior e enxerga um perfil sequencial de interferência luminosa composta por 6 franjas escuras e 5 franjas claras ao longo da extensão do filme, onde as franjas nas extremidades são escuras. Considere a incidência normal dos raios de luz.
(a) Obtenha as condições para interferência construtiva e destrutiva da luz observada para uma dada espessura y tal que
(b) Calcule a diferença em termos de e
Passo 1
(a) Vamos começar lembrando que, quando temos filmes finos, o fato de haver interferência construtiva ou destrutiva depende da diferença de fase total.
Ela é dada pela soma de uma diferença de fase devido à diferença de caminho ótico e outra diferença de fase devido à reflexão:
A diferença de fase devido à diferença de caminho, numa espessura y do filme, é dada por:
onde:
A diferença de fase devido à reflexão vale , quando a luz passa do ar para o plástico, e 0 quando a luz passa do plástico para o ar, pois .
O raio 1 vai se defasar em radianos, pois ele vem da reflexão da luz do ar para o plástico.
O raio 2 teve antes uma reflexão do plástico para o ar, então a diferença de fase é 0, e depois teve uma difração, que não tem diferença de fase associada.
Logo a diferença de fase devido à reflexão é só mesmo:
Logo:
Passo 2
Para haver diferença construtiva, a diferença de caminho total tem que ser um múltiplo inteiro de :
com
Substituindo:
Dividindo os dois lados por
com
Já para a interferência destrutiva:
com
Substituindo:
Dividindo os dois lados por
com
Passo 3
(b) O enunciado disse que as extremidades do filme eram franjas escuras, ou seja, eram pontos de interferência destrutiva.
Como também foi dito que há 6 franjas escuras, a extremidade equivale a na e a extremidade equivale a
Substituindo essas condições na fórmula de interferência destrutiva que achamos no item (a):
Subtraindo a equação de cima da de baixo:
Resposta
(a) Interferência construtiva: ,
Interferência destrutiva:
(b)