Uma película de sabão ) com de espessura é iluminada perpendicularmente com luz branca. Para quantos comprimentos de onda diferentes na faixa de a a luz refletida apresenta (a) interferência construtiva total e (b) interferência destrutiva total?
Passo 1
A questão trata sobre interferência em filmes finos. A figura ilustra a situação com um filme fino de sabão cuja espessura é entre duas camadas de ar.
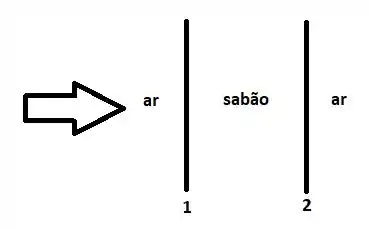
No caso temos que . Assim, na reflexão que ocorre na interface 1 há mudança de fase enquanto que na interface 2 não há. Assim, além da diferença de caminho, devemos somar na defasagem entre as ondas:
A diferença de caminho é (dobro da espessura da camada de sabão) e o fator que foi somada é devido ao fato de em uma das reflexões a fase ter invertido enquanto na outra não! É importante lembrar que:
Passo 2
No item (a) queremos que a interferência seja construtiva, de modo que a fase deve ser múltipla inteira de :
Portanto,
Como queremos saber quantos comprimentos de onda estarão na faixa entre e , tomando :
Para :
Assim, os valores possíveis de para que o comprimento de onda esteja na faixa visível são
Portanto, para quatro comprimentos de onda a interferência será construtiva!
Passo 3
Já para interferência destrutiva, devemos ter
Assim,
Para :
Já para :
Assím, nessa faixa, os valores de para que a interferência seja destrutiva são
Portanto, são três comprimentos de onda!
Resposta
Construtiva: 4
Destrutiva: 3