Considere uma espira circular, de raio , na presença de um campo magnético constante (uniforme e estacionário) , como mostra a figura. O vetor unitário , perpendicular ao plano da espira, forma um ângulo com o vetor unitário . Através da espira, circula uma corrente estacionária de intensidade , no sentido anti-horário. Determine o fluxo do campo magnético através da espira, o módulo da força magnética e o módulo do torque resultantes sobre ela.
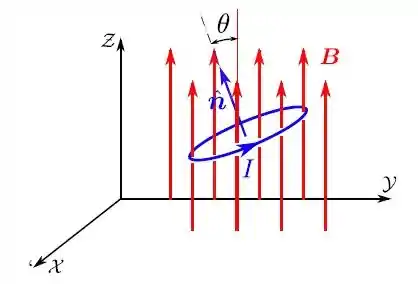
- , ,
- , ,
- , ,
- , ,
- , ,
- , ,
Passo 1
A fórmula do fluxo magnético é:
Fazendo o produto escalar:
Como o módulo de é constante e o ângulo também:
A área da espira é conhecidamente :
Passo 2
Depois disto vamos calcular o torque pois é mais fácil:
Onde é o vetor momento de dipolo, que é o produto do vetor área pela corrente:
Passo 3
Sabendo que , fazemos o produto vetorial puxando as constantes para fora:
Aplicando a definição do produto vetorial:
Onde é o unitário que dá a direção do produto calculado. Nós não sabemos pra onde ele aponta, mas tampouco isto importa, pois queremos o módulo:
Passo 4
Dados esses valores encontrados podemos analisar as alternativas e ver que a única possível é a letra e. Mas para efeito didático vamos calcular a força...
A força magnética sobre a espira pode ser calculada com a expressão:
Temos que é um vetor infinitesimal de trajetória tangente à espira em todos os pontos:
Passo 5
Fazendo o produto vetorial:
Que resulta em:
Realizando a integral, lembrando que ela é fechada pois a espira é um circuito fechado:
Passo 6
Na integral de um circuito fechado o primeiro ponto é igual ao último:
Logo:
Pela definição de integral:
Ou seja, a força de um campo estacionário num circuito fechado é nula.
Resposta
Letra e