![]()
![]()
Passo 1
Primeiramente, vamos relembrar como calculamos o limite de uma sequência :
No nosso caso, ficamos com:
Se esse limite existe e for um número, a sequência converge e o limite dela é este número. Caso contrário, ela diverge.
Passo 2
Eu sei que é muito confortável a gente fazer esse limite direto, do jeito que está escrito, porque aí ficamos com:
Mas isso às vezes pode parecer meio chutado, é importante que você avalie como fração, digamos que tem menos culpa hahaha. O truque aqui é a gente manipular de forma que apareça um produto notável:
Foi para zero pois o denominador estava indo pro infinito e temos um número constante no numerador. Olhe o gráfico dessa sequência, mas pense como se ela fosse função (ou seja, estou considerando valores de que não sejam apenas inteiros):
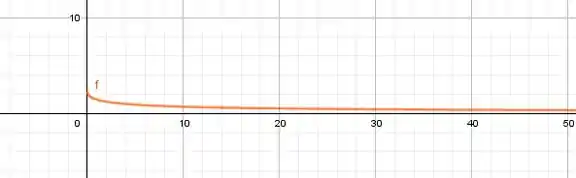
Está tendendo pra zero, percebe? Então nosso limite faz sentido!