UnB – Cálculo 1 – Lista de Exercícios 14 – Questão 6a
Após identificar a técnica apropriada, determine o valor das integrais abaixo
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas vou te ajudar!
O problema nos deu essa integral aqui
E pediu para resolvermos! Ué, mas por onde começar? Olhando sempre na tabela! Se você logo de cara não identificar uma fórmula que se adeque, então precisamos usar alguma técnica!
Beleza? Como não encontramos nenhuma fórmula da tabela, vamos aos métodos! Começando pelo método da substituição: nele a gente tenta encontrar uma parte do integrando para chamar de e que o restante do integrando tenha a sua derivada
Anota aí!
E é ela que vamos aplicar aqui!
e é isso! Mas relaxa que vou fazer passo a passo com você!
Vamos começar?
Passo 2
Nossa integral é a seguinte
Mas se chamarmos de o argumento da exponencial , quando derivarmos
Vamos ter (a menos de uma constante) o restante do integrando:
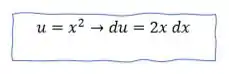E é isso! Essa é nossa substituição
Nosso integrando vai ficar assim:
Agora é #partiu integrar!
Passo 3
Agora vamos integrar
E por fim, precisamos retornar para . Lembrando que
Não esqueça de colocar o no final da integral! Estamos calculando uma integral indefinida!
E é isso! Espero ter ajudado!