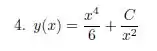![]()
![]()
Passo 1
A primeira coisa é identificar se nossa equação é linear de primeira ordem. Os pré-requisitos para isso são:
Para ser de primeira ordem a derivada de maior ordem deve ter ordem 1.
Ok, de primeira ordem ela é. Mas para ser linear:
- Tanto as derivadas de quanto o próprio não podem estar elevados ao quadrado, cubo ou qualquer outro expoente diferente de 1.
- Os coeficientes que aparecem multiplicando as derivadas de e o próprio dependem apenas de .
Está tudo de acordo, temos uma equação linear de primeira ordem.
Passo 2
Agora vamos resolvê-la. Essa é uma EDO não é separável. E agora? Mas ela parece aquelas EDOs exatas. Vamos confirmar?
Um EDO exata tem esse formato aqui
E para comprovar se ela é exata é preciso satisfazer a condição
No caso da nossa equação
Putz ! Não temos uma equação exata. Mas tá quase lá, então podemos encontrar um fator integrante para ela se tornar exata.
Passo 3
Vamos encontrar esse tal de fator integrante. Há duas possibilidades
Candidato 1
Candidato 2
O fator integrante deve ser função ou só de ou só de . Então nossa melhor escolha é o candidato 1.
Para saber o fator integrante mesmo, precisamos fazer
Então
Passo 4
Agora precisamos multiplicar os termos da equação pelo fator integrante, conferir se ficou exata mesmo e depois resolver a edo.
Multiplicando pelo fator integrante
Então
Agora sim é uma equação exata e podemos resolver.
Passo 5
Primeiro precisamos calcular
Para encontrar vamos derivar a integral que calculamos em função de e depois comparar com e integrar novamente.
Passo 6
Por fim, só falta comprar nosso resultado com a constante de integração.
Agora sim, fim!
Resposta