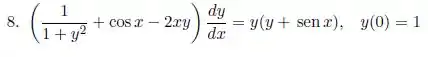Exercícios de Equação Exata - Lista de Exercícios Resolvida

Resolva a equação diferencial

Resolva a seguinte equação exata:

Resolva a equação diferencial.

Resolva o problema de valor inicial abaixo, isto é, encontre a função ou as funções que satisfaz(em) a equação diferencial e a condição inicial dadas.

Determine todas as funções que tornam exata a equação diferencial

Considere a função tal que e encontre a solução geral da equação dada em

Verifique que a equação é exata e resolva-a

Para cada uma das EDOs a seguir, verifique que ela é exata e então determine a sua solução geral.

(7)

Para cada uma das EDOs a seguir, verifique que ela é exata e então determine a sua solução geral.

(9)

Considere a equação

Encontre tal que a equação acima esteja na forma exata;

Encontre uma solução para a equação utilizando a função encontrada no item anterior;

Prescreva uma condição inicial e encontre a solução do associado.

Dica: considere integração por partes se for preciso calcular a integral de .

Resolva a ED exata:

Nos exercícios de a identifique as equações diferenciais exatas e resolva-as.

Nos exercícios de a identifique as equações diferenciais exatas e resolva-as.

Nos exercícios de a identifique as equações diferenciais exatas e resolva-as.

Nos exercícios e resolva o .

Nos exercícios de a identifique as equações diferenciais exatas e resolva-as.

Nos exercícios de a identifique as equações diferenciais exatas e resolva-as.

Resolva os seguintes problemas de valor inicial

a)

Considere a equação diferencial

1. Encontre a solução geral da equação diferencial
2. Resolva o problema de valor inicial dado com

Prove que a seguinte equação diferencial é exata e resolva-a:

Resolva as seguintes equações diferenciais ou problemas de valor inicial, conforme seja o caso.

b)

Resolva o problema de valor inicial abaixo, insto é, encontre a função ou as funções que satisfaz(em) a equação diferencial e as condições iniciais dadas.

Considere a equação diferencial

1. Determine todas as funções que tornam exata a equação diferencial
2. Encontre a solução geral da equação diferencial usando a achada no item .

Resolva o problema de valor inicial abaixo, isto é, encontre a função ou as funções que satisfaz(em) a equação diferencial e as condições iniciais dadas.

Como vimos em sala, a equação

é exata, cujo método de resolução leva a solução implícita . Obtenha a solução pelo método para equação com coeficientes lineares.

Como vimos em sala, a equação

Obtenha a solução pelo método de equações exatas;

Considere o seguinte ,

Verifique que a EDO associada ao dado é exata.

Calcule a solução do ,(use o fato que constante). Depois, responda se a solução calculada é única ou não, justificando sua resposta.

Encontre a solução geral da equação diferencial:

Para cada uma das EDOs a seguir, verifique que ela é exata e então determine a sua solução geral.

(8)

Questão 1: Resolva as seguintes equações diferenciais e problemas de valor inicial, conforme seja o caso:

Teste 5: Considere a equação

Onde são funções . Seja um fator integrante da equação e um potencial correspondente, ou seja: é derivável e . Qual das funções abaixo é outro fator integrante para a equação diferencial?

Questão 1: Resolva as seguintes equações diferenciais ou problemas de valor inicial, conforme seja o caso.

A ordem de uma equação diferencial é a ordem da derivada de maior ordem que aparece na equação. Com relação às equações diferenciais de primeira ordem é SOMENTE correto afirmar que

(I) A forma geral das equações diferenciais de 1ª ordem é .

(II) São equações de 1ª ordem e 1° grau as equações da forma:

(III) São equações de 1ª ordem e 1° grau as equações da forma onde e são contínuas no intervalo considerado.

( )(I), (II) e (III)

( ) (III)

( ) (II)

( ) (I)

( ) (I) e (II)

Verifique se a equação diferencial é exata

( )

( )

( )

( )

( )

A solução da equação diferencial é

( )

( )

( )

( )

( )

Responda as questões abaixo JUSTIFICANDO.

a) Exiba uma equação exata que admita como soluções a família de curvas

b) Ache a solução particular quando

Questão 1:

Considere as variáveis e relacionadas pela forma diferencial:

Encontre o valor de para que o qual a equação acima seja exata.

Classifique as equações diferenciais de 1ª ordem abaixo:

Classifique as equações diferenciais de 1ª ordem abaixo:

Determine explicitamente, ou indique implicitamente, a solução do problema de

valor inicial para cada equação diferencial de 1ª ordem acima, com a condição inicial :

Determine explicitamente, ou indique implicitamente, a solução do problema de

valor inicial para cada equação diferencial de 1ª ordem acima, com a condição inicial :

Determine se a ED dada é exata e, então, resolva:

Como vimos em sala, a equação

Obtenha a solução pelo método das equações com coeficientes lineares.

Resolva a equação diferencial não-linear , , considerando a teoria sobre equações exatas.

1) Resolva a EDO .

3) Achar um fator integrante da equação .

Determine as soluções gerais, explicitas ou implícitas, das equações diferenciais

de 1ª ordem acima, com métodos apropriados para cada caso.

b)

Determine as soluções gerais, explicitas ou implícitas, das equações diferenciais

de 1ª ordem acima, com métodos apropriados para cada caso.

Questão 1 (Justifique todas as suas respostas):

Encontre o valor de para o qual a equação dada é exata e depois a resolva usando este valor de .

Resolva a seguinte equação diferencial ou problema de valor inicial conforme caso abaixo:

4) Determinar a EDO exata que tenha como solução geral a equação dada.

a)

4) Determinar a EDO exata que tenha como solução geral a equação dada.

b)

5) Verificar que a EDO é exata e resolvê-la.

a)

5) Verificar que a EDO é exata e resolvê-la.

c)

5) Verificar que a EDO é exata e resolvê-la.

e)

5) Verificar que a EDO é exata e resolvê-la.

f)

5) Verificar que a EDO é exata e resolvê-la.

b)

5) Verificar que a EDO é exata e resolvê-la.

d)

6) Resolver os Problemas de Valor Inicial.

a) , .

Nos exercícios de a identifique as equações diferenciais exatas e resolva-as.

Encontre o valor de para o qual a equação dada é exata e depois a resolva usando este valor de :

Dadas as EDOs abaixo, determine quais são exatas.

I-

II-

III-

( ) Apenas a II

( ) Apenas a III

( ) Apenas a I

( ) I, II e III são exatas.

( ) I, II e III são não exatas.

Para cada equação, determine se ela é exata. Se for, encontre a solução:

b)

A condição necessária e suficiente para que a equação seja diferencial exata é que, sendo e funções contínuas e deriváveis, se tenha .

Resolva a equação exata

Encontre uma solução para a seguinte equação exata:

Resolve as seguintes equações diferenciais. No caso da letra a), resolve o problema de valor inicial associado.

Considere o problema de valor inicial

Qual o limite de quando tende a ?

Encontre o valor de para o qual a equação dada é exata e depois a resolva usando este valor de :

Encontre o valor de para o qual a equação dada é exata e depois a resolva usando este valor de :

Uma equação diferencial é chamada de exata se:

( )

( )

( )

( )

( )

Seja uma função contínua em um intervalo e sejam e funções diferenciáveis cujos valores estão em . Prove que

A fórmula acima é conhecida como Regra de Leibniz.

Para cada uma das EDO’s a seguir, verifique que ela é exata e então determine sua solução geral.

1.

Para cada uma das EDO’s a seguir, verifique que ela é exata e então determine sua solução geral.

2.

Para cada uma das EDO’s a seguir, verifique que ela é exata e então determine sua solução geral.

3.

Para cada uma das EDO’s a seguir, verifique que ela é exata e então determine sua solução geral.

4.

Para cada uma das EDO’s a seguir, verifique que ela é exata e então determine sua solução geral.

5.

Para cada uma das EDO’s a seguir, verifique que ela é exata e então determine sua solução geral.

6.

Determine se a equação dada é exata. Se for, encontre a solução.

Determine se a equação dada é exata. Se for, encontre a solução.

Determine se a equação dada é exata. Se for, encontre a solução.

Determine se a equação dada é exata. Se for, encontre a solução.

Sejam contínua com , para todo ,

e

tais que a área de A ∩ B seja igual a 23. Calcule

Sabe-se que é uma função contínua que satisfaz a equação para todo x > 0 e algum a > 0. Dado t > 0, qual é o valor de f(t)?