Três cargas puntiformes estão dispostas ao longo do eixo . A carga está na origem e a carga está em . A carga . Onde estará localizado quando a força resultante sobre for no sentido ?
Passo 1
Se tomarmos a liberdade de desenhar essa bagaça, vamos poder começar a entender melhor o problema:
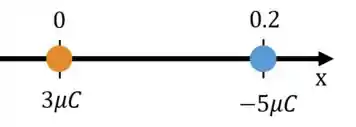
Lembrando que não precisa colocar o no desenho pois sua posição é desconhecida. Você pode até colocar, mas contanto que isso não te sugestione a pensar que a carga deve ficar necessariamente na parte positiva do eixo (que é o que 90% das pessoas fazem).
Podemos ver que, pelo sinal das cargas, a força em é atrativa e portanto aponta para a direita ().
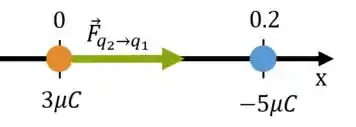
Passo 2
Do enunciado, sabemos que a resultante em é no sentido de , portanto:
Uma vez que tenhamos uma dessas forças, podemos calcular a outra.
Passo 3
Podemos aplicar a Lei de Coulomb para achar a força resultante em , onde nossa incógnita é a distância entre e , pois a posição de é desconhecida.
Plugando os valores, e sabendo que o vetor unitário (que aponta da carga que faz a força para aquela que sofre a força) no eixo é o nosso (menos xis chapéu).
Fazendo de cabeça:
Passo 4
Aplicando esse valor encontrado na equação da resultante:
Agora show. Como a carga e tem sinais opostos, sabemos que ela fazem uma força atrativa entre si. Logo, o único jeito dela fazer uma força atrativa no sentido de é estando na parte negativa do eixo :
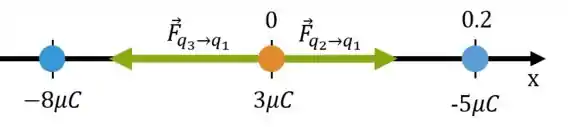
Se não se convenceu tente colocar ela em outra posição.
Passo 5
Aplicando a mesma lógica para as cargas e :
Neste caso, tratar com o módulo do vetor facilita nossa vida:
Sabendo que o é a nossa incógnita desejada:
Isolamos:
Plugamos os valores:
Como já conseguimos inferir que deve estar na parte negativa do eixo , substituímos: