Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança Qualquer de Variáveis

Ver Teoria
Exercício 4912345678910111213141516171819202122232425262728293031323334353637383940414243444546474850515253545556575859606162636465666768697071727374757677787980818283

Enunciado

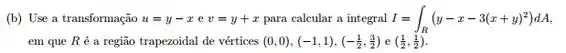
Passo 1

Antes de usar a transformação que nem o enunciado falou, vamos tentar entender que região R tem esses pontos aí:

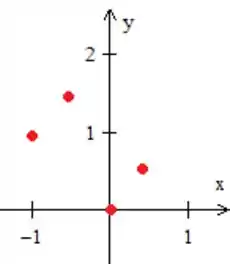
Ligando todos eles a gente fica com

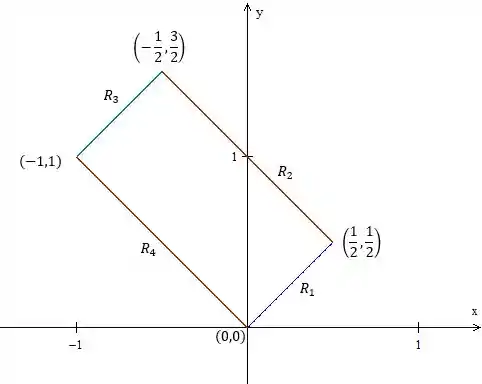
O grande desafio aqui é descobrir as equações dessas quatro retas. Pra isso a gente pode usar os pontos dados pelo enunciado, olha só, vamos começar com R 1 :

y = A x + B

0,0 → 0 = 0 + B 1 2 , 1 2 → 1 2 = A 2 + B

B = 0

A 2 = 1 2

A = 1

Logo

R 1 : y = x

Repetindo esse procedimento pra R 2

y = A x + B

1 2 , 1 2 → 1 2 = A 2 + B - 1 2 , 3 2 → 3 2 = - A 2 + B

Subtraindo as duas equações:

1 2 - 3 2 = A 2 - - A 2

A = - 1

B = 1

Logo

R 2 : y = - x + 1

Agora em R 3

y = A x + B

- 1 2 , 3 2 → 3 2 = - A 2 + B - 1,1 → 1 = - A + B

Subtraindo as duas equações:

3 2 - 1 = - A 2 - - A

A = 1

B = 2

Logo

R 3 : y = x + 2

Por fim, fazendo para R 4

y = A x + B

- 1,1 → 1 = - A + B 0,0 → 0 = B

B = 0

A = - 1

Logo

R 4 : y = - x

Nosso esboço final fica assim

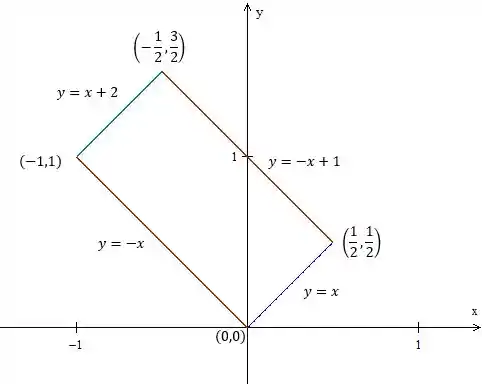
Passo 2

Depois de toda essa análise, vamos pensar em como usar a mudança de variáveis que o enunciado falou:

u = y - x

v = y + x

Percebe que podemos reescrever as quatro retas como:

y = x → y - x = 0 → u = 0

y = - x + 1 → y + x = 1 → v = 1

y = x + 2 → y - x = 2 → u = 2

y = - x → y + x = 0 → v = 0

Ou seja, essa região fica muito mais simples escrita em u e v !

0 ≤ u ≤ 2

0 ≤ v ≤ 1

Passo 3

Agora que analisamos a região inteira e transformamos em u e v , falta a gente fazer o mesmo com a parte de dentro da integral:

I = ∫ R y - x - 3 x + y 2 d A

I = ∫ R u - 3 v 2 d A

Passo 4

Por fim, antes de fazer as contas, não podemos esquecer do jacobiano!

J = ∂ x , y ∂ ( u , v )

Ou podemos fazer pelo método alternativo com o inverso do jacobiano

J * = 1 | J | = ∂ u , v ∂ x , y

∂ u ∂ x = ∂ y - x ∂ x = - 1

∂ u ∂ y = ∂ y - x ∂ y = 1

∂ v ∂ x = ∂ y + x ∂ x = 1

∂ u ∂ y = ∂ y + x ∂ y = 1

Juntando tudo e jogando no determinante do jacobiano:

J * = - 1 1 1 1 = - 2

J = 1 | - 2 | = 1 2

Passo 5

Agora sim podemos calcular a integral dupla

I = ∫ R u - 3 v 2 d A

= ∫ 0 2 ∫ 0 1 u - 3 v 2 1 2 d v d u

= 1 2 ∫ 0 2 u v - 3 v 3 3 v = 0 v = 1 d u

= 1 2 ∫ 0 2 u - 1 d u

= 1 2 u 2 2 - u u = 0 u = 2

= 1 2 2 - 2

= 0

Tudo isso pra dar zero...

Resposta

0

Exercícios de Livros Relacionados

Determine o jacobiano da transformação.x = v + w^2 , y = w + u^2 , z = u + v^2
Calcule a integral, efetuando uma mudança de variáveis apropriada. ∫ ∫ R x - 2 y 3 x - yd A , onde R é o paralelogramo delimitado pelas retas x - 2 y = 0, x - 2 y = 4, 3 x - y = 1, 3 x - y = 8
Utilize a transformação dada para calcular a integral. ∬ R 4 x + 8 y d A , onde R é o paralelogramo com vértices - 1,3 , 1 , - 3 , 3 , - 1 e 1,5 ; x = 1 4 u + v , y = 1 4 v - 3 u
Calcule ∫ ∫ D y + 2 x y - 2 x - 1 d x d y , onde D é a região do plano x y limitada por y - 2 x = 2 , y + 2 x = 2 , y - 2 x = 1 e y + 2 x = 1 .
Calcule ∫ ∫ D xd x d y , onde D é a região do plano x y limitada pelas parabolas x = y 2 - 1 , x = 1 - y 2 e x = 4 - y 2 4 .