Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança Qualquer de Variáveis

Ver Teoria
Exercício 8212345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808183

Enunciado

UTFPR, Sem Campus, Cálculo Diferencial e Integral 2, AV3 - 2022.1

Calcule, utilizando uma mudança de variáveis conveniente, a integral

∬ x + y 6 y - x d A

Sendo D a região limitada pelas retas y + x = 3 , y + x = 5 , y - x = 1 e y - x = 3 .

Passo 1

A primeira coisa que iremos fazer meu caro colega é desenhar a região de integração D por meio do Geogebra.

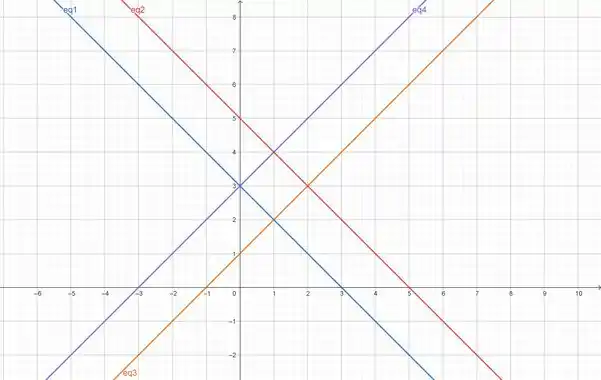
Passo 2

A nossa região de integração é o nosso querido quadrado formado pelas quatro retas da figura. Acredito que você assim como eu notou que teremos que dividir nossa integração em duas.

Da origem até a linha preta x = 1

∫ 2 4 ∫ 3 - y y - 3 x + y 6 y - x d x d y

Passo 3

Vamos partir para resolver a integral com uma substituição de varial, tal que u = x + y e v = y - x , e podemos rescrever em termos de u   e   v da seguinte forma, u + v 2 = y e u - v 2 = x .

Temos que

J = ∂ x , y ∂ u . v = ∂ x ∂ u ∂ x ∂ v ∂ y ∂ u ∂ y ∂ v = 1 2 - 1 2 1 2 1 2 = 1 4 + 1 4 = 1 2

Precisamos agora lidarmos com os intervalos de integração, já que mudamos de variável

y + x = 3 → u = 3

y + x = 5 → u = 5

y - x = 1 → v = 1

y - x = 3 → v = 3

Agora finalmente poderemos calcular a integral

1 2 ∫ 1 3 ∫ 3 5 u 6 v d u d v

∫ 3 5 u 6 v d u = u 7 7 ​ 3 5

= 5 7 7 - 5 3 7

= 78000 7

= 1 2 ∫ 1 3 78000 v 7 d v

= 78000 14 ln ⁡ 3

Agora note que até onde calculamos, temos uma simetria, sendo assim poderemos apenas multiplicar nosso resultado encontrado por 2, então

78000 7 ( ln ⁡ 3 )

E aqui terminamos nossa resolução, um forte abraço meu caro colega e até uma próxima.

Resposta

= 78000 7 ln ⁡ 3

Exercícios de Livros Relacionados

Determine o jacobiano da transformação.x = v + w^2 , y = w + u^2 , z = u + v^2
Calcule a integral, efetuando uma mudança de variáveis apropriada. ∫ ∫ R x - 2 y 3 x - yd A , onde R é o paralelogramo delimitado pelas retas x - 2 y = 0, x - 2 y = 4, 3 x - y = 1, 3 x - y = 8
Utilize a transformação dada para calcular a integral. ∬ R 4 x + 8 y d A , onde R é o paralelogramo com vértices - 1,3 , 1 , - 3 , 3 , - 1 e 1,5 ; x = 1 4 u + v , y = 1 4 v - 3 u
Calcule ∫ ∫ D y + 2 x y - 2 x - 1 d x d y , onde D é a região do plano x y limitada por y - 2 x = 2 , y + 2 x = 2 , y - 2 x = 1 e y + 2 x = 1 .
Calcule ∫ ∫ D xd x d y , onde D é a região do plano x y limitada pelas parabolas x = y 2 - 1 , x = 1 - y 2 e x = 4 - y 2 4 .