UFU, Sem Campus, Cálculo 2, Listas de C2 - Profª Ana Paula - Lista 7 - Integrais Duplas, Questão 16a
Utiliza a transformação dada para calcular a integral
a) , onde é a região triangular com vértices , e ; , .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular a integral dupla sobre o triângulo de vértices , e , usando a transformação e . Nosso triângulo, então, é esse aqui:
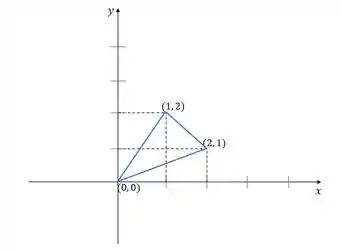
Repare que cada reta que forma o triângulo pode ser descrita por uma função do tipo . E nós vamos precisar encontrar as expressões que definem essas funções, para definir a nossa região de integração.
Depois disso, para calcular essa integral, vamos usar a definição:
Onde é o Jacobiano da transformação, que é dado da seguinte forma:
Então, vamos calcular as derivadas parciais de e , tirar esse determinante e substituir na integral junto com os intervalos de integração e nossa escrita em função de e .
Vamos lá!
Passo 2
Vamos começar calculando as derivadas do nosso jacobiano.
Temos que é a derivada de em função de :
E é a derivada de em função de :
Temos que é a derivada de em função de :
E por ultimo é a derivada de em função de :
Passo 3
Pronto, agora é só substituir e calcular:
Passo 4
A transformação mapeia o limite de para o limite da imagem . Então, vamos encontrar as funções que definem as retas do nosso triângulo, visto no passo , e substituir as equações de transformação, e .
A reta com os pontos e é , que tem uma imagem:
A reta com os pontos e é , que tem uma imagem:
A reta com os pontos e é , que tem uma imagem:
Agora temos e no plano .
Passo 5
Agora vamos substituir na integral:
Integrando primeiro em relação a :
E aplicando os limites de integração em :
Agora integrando em relação a :
E aplicando os limites de integração em :
Valeu, galera! Até a próxima! 😉