Calcule
Sendo a região do plano limitada por , , , .
Passo 1
Parece bem difícil essa integral né? Mas perceba que o termo aparece tanto na integral quanto nos limites de integração, isso já nos faz imaginar que vamos ter que fazer uma mudança de variável!
O que vamos fazer agora é a parte chave da questão! Escolher as novas variáveis da forma certa vai facilitar muito nosso trabalho, precisamos analisar tudo no nosso enunciado antes de tomar uma decisão.
Perceba que o outro termo da integral, , pode ser escrito novamente da seguinte forma:
Ótimo! Nosso termo apareceu de novo, só que multiplicado por . Não é problema, só fazer:
Somando as duas equações:
Passo 2
Agora que escolhemos nossas novas variáveis, o próximo passo é calcular o jacobiano:
Só que lembra que jacobiano sempre é positivo! Logo
Passo 3
Vamos descobrir nossos limites em e , é só substituir nossas variáveis nos limites que tínhamos antes:
No gráfico vamos ter:
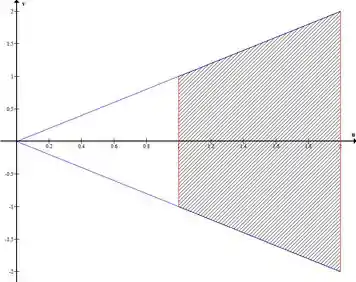
Portanto, temos nossos novos limites como:
Passo 4
Reescrevendo nossa integral com os novos limites e o jacobiano:
Passo 5
Vamos integrar em primeiro então:
Para facilitar nossas contas, vamos usar a relação que diz que
Integrando em agora, vamos fazer uma substituição rápida: