Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança Qualquer de Variáveis

Ver Teoria
Exercício 4312345678910111213141516171819202122232425262728293031323334353637383940414244454647484950515253545556575859606162636465666768697071727374757677787980818283

Enunciado

Mudança de variáveis

Seja R a região plana no primeiro quadrante compreendida pelo gráfico das funções y = x 2 , y = x , y = 1 x e y = 2 x .

  1. Usando a mudança de variáveis u = x y e v = y / x , determine a transformação T = T ( u , v ) e calcule a matriz jacobiana de T .
  2. Determine a região S do plano u v cuja imagem pela transformação T é R .
  3. Use a fórmula de mudança de variávies para provar que

∬ R   f x y d A = ln ⁡ 2

Onde f : R → R é uma função tal que

∫ 0 1 2 ln ⁡ 2 2 f e 2 x e 2 x d x = 2

Passo 1

a)

Temos a seguinte mudança de variáveis:

u = x y

v = y / x

Isolando x e y , temos

x = u v

y = u v

x , y = T u , v = u v , u v

O que nos dá

∂ x ∂ u = 1 2 u v  

∂ x ∂ v = - u 2 v v

∂ y ∂ u = v 2 u

∂ y ∂ v = u 2 v

Como

J = ∂ ( x , y ) ∂ ( u , v )     = ∂ x ∂ u ∂ x ∂ v ∂ y ∂ u ∂ y ∂ v

J = 1 2 u v - u 2 v v v 2 u u 2 v = 1 4 v + 1 4 v = 1 2 v

J = 1 2 v

Passo 2

Letra b)

Agora temos que descobrir nossa região de integração no plano u v . No plano x y , sabemos que ela é limitada pelas funções y = x 2 , y = x , y = 1 x e y = 2 x . Aplicando a mudança, temos:

u = x y

v = y / x

y = x 2             →             v = 1 2

y = x             →             v = 1

y = 1 x             →             u = 1

y = 2 x             →             u = 2

Show? Agora vamos levar isso para um gráfico:

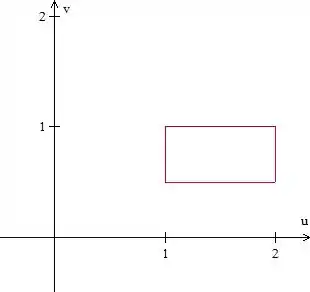
Logo, S = 1,2 × 1 2 , 1 .

Passo 3

Letra c)

Bom, dá pra ver que T não é uma função injetora:

x , y = T u , v = u v , u v

Já que T u , v = T ( - u , - v ) . Ou seja, dois pontos diferentes possuem mesma imagem. Porém, se considerarmos apenas o conjunto de pontos dentro do retângulo (a região S do passo anterior), então não temos esse problema. E podemos fazer a transformação.

Já temos que o Jacobiano dessa transformação é:

J = 1 2 v

Usando a fórmula da mudança de variáveis então:

∬ R   f x y d A = ∫ 1 2 ∫ 1 / 2 1 f u 1 2 v d v d u

= 1 2 ∫ 1 2 f u ln ⁡ v 1 / 2 1 d u =

= 1 2 ∫ 1 2 f u ln ⁡ 1 - ln ⁡ 1 2 d u =

= 1 2 ∫ 1 2 f u ln ⁡ 1 - ln ⁡ 2 - 1 d u =

= 1 2 ∫ 1 2 f u 0 + ln ⁡ 2 d u =

= 1 2 ∫ 1 2 f u ln ⁡ 2 d u =

= ln ⁡ 2 2 ∫ 1 2 f u d u

Então

∬ R   f x y d A = ln ⁡ 2 2 ∫ 1 2 f ( u ) d u

Chegamos na integral dupla que queríamos, vamos no próximo passo dar uma arrumada na integral que ele deu.

Passo 4

Ele disse no enunciado que

∫ 0 1 2 ln ⁡ 2 2 f e 2 x e 2 x d x = 2

Podemos começar tirando aquele 2 da integral, fazendo

2 ∫ 0 1 2 ln ⁡ 2 f e 2 x e 2 x d x = 2

∫ 0 1 2 ln ⁡ 2 f e 2 x e 2 x d x = 1

Queremos que esse cara fique parecido com aquele que achamos, para que isso tudo faça sentido, então queremos f u ali dentro, nada mais interessante que fazer o cara dentro da f sendo u

u = e 2 x

d u = 2 e 2 x d x

d u 2 = e 2 x d x

Vamos agora mudar os limites de integração

x = ln ⁡ 2 2 → u = e 2 x → u = e 2 ln ⁡ 2 2 = e ln ⁡ 2 = 2

x = 0 → u = e 2 x → u = e 2 . 0 = e 0 = 1

Então a integral vai ficar

∫ 0 1 2 ln ⁡ 2 f e 2 x e 2 x d x = ∫ 1 2 f u d u 2 = 1 2 ∫ 1 2 f u d u

Lembrando que isso é 1

Então

1 2 ∫ 1 2 f u d u = 1

∫ 1 2 f u d u = 2

Passo 5

Vamos agora juntar a toda essa bagunça, achamos no passo 3 que

∬ R   f x y d A = ln ⁡ 2 2 ∫ 1 2 f ( u ) d u

E no passo 4 que

∫ 1 2 f u d u = 2

Então

∬ R   f x y d A = ln ⁡ 2 2 ∙ 2 = ln ⁡ 2

Como ele queria demostrar.

Vale um comentário aqui, na prova que conseguimos essa questão está totalmente errada, ele faz um conta matemática completamente errada, em vez desse monte de ln ⁡   que colocamos ele coloca log ⁡   , ou seja, na base 10 , vamos ignorar esse detalhe, pelo gabarito isso foi erro de digitação deles mesmo.

Resposta

  1. x , y = T u , v = u v , u v ;   J = 1 2 v
  2. S = 1,2 × 1 2 , 1

Exercícios de Livros Relacionados

Determine o jacobiano da transformação.x = v + w^2 , y = w + u^2 , z = u + v^2
Calcule a integral, efetuando uma mudança de variáveis apropriada. ∫ ∫ R x - 2 y 3 x - yd A , onde R é o paralelogramo delimitado pelas retas x - 2 y = 0, x - 2 y = 4, 3 x - y = 1, 3 x - y = 8
Utilize a transformação dada para calcular a integral. ∬ R 4 x + 8 y d A , onde R é o paralelogramo com vértices - 1,3 , 1 , - 3 , 3 , - 1 e 1,5 ; x = 1 4 u + v , y = 1 4 v - 3 u
Calcule ∫ ∫ D y + 2 x y - 2 x - 1 d x d y , onde D é a região do plano x y limitada por y - 2 x = 2 , y + 2 x = 2 , y - 2 x = 1 e y + 2 x = 1 .
Calcule ∫ ∫ D xd x d y , onde D é a região do plano x y limitada pelas parabolas x = y 2 - 1 , x = 1 - y 2 e x = 4 - y 2 4 .