Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança Qualquer de Variáveis

Ver Teoria
Exercício 5512345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535456575859606162636465666768697071727374757677787980818283

Enunciado

Seja B   a região triangular do plano u v com vértices nos pontos - 1 ,   1 ,   0 ,   0   e ( 0 ,   1 ) .

  1. Considere a mudança de variáveis T u ,   v = ( u - v ,   v 3 ) e esboce a região D do plano x y tal que T B = D
  2. Calcule o Jacobiano da mudança de variáveis
  3. Seja a função

f : D →   R

x ,   y ⟼ 3 π 2 4 x + y 3 2 ∙ sin ⁡ π 2 y

Calcule a integral ∬ D f x , y d x d y .

Passo 1

Letra a) Para a gente entender melhor como vamos encontrar a região pedida D , você não acha que é válido olhar melhor para esse triângulo aí?

Então, se a gente colocar esses vértices no plano u v e desenharmos os lados dele, vamos obter

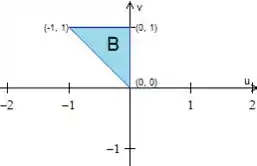
Bem... para gente desenhar os limites da nossa nova superfície vamos fazer a seguinte substituição x = u - v e y = v 3 , assim teremos T u ,   v = u - v ,   v 3 = ( x ,   y )

Okay! Mas quem são os limites dessa nova superfície D ?!

Para responder essa questão, vamos olhar para os limites dessa região B acima e ver no que a gente consegue como limite na nova região x y , beleza?!

Passo 2

Bem... sabemos que a reta perpendicular ao eixo O u que delimita o triângulo é do tipo u = 0 , logo

x = - v y = v 3 ⇒     y = - x 3 = - x 3

Porem, v varia de 0 a 1 então x = - v varia de - 1 até 0 , ou seja, x ∈ - 1 ,   0

Uma outra reta que delimita B é a reta inclinada onde podemos perceber que u = - v . Assim, teremos

x = - 2 v y = v 3 ⇒    

Isolando v e jogando no valor de x ...

y = - x 2 3 = - x 3 8

Ganhamos a nossa outra curva que delimita a nossa nova região e seus limites são v ∈ 0 ,   1 logo, como x = - 2 v , x ∈ - 2 ,   0

Por fim, vemos que nossa última delimitação para B é v = 1 , portanto, sendo y = v , teremos y = 1 e x = u - v está livre variando de - 2 á -1, pois

v = 1 x = u - v ⇒ P a r a   u = - 1   x = - 2

E

v = 1 x = u - v ⇒ P a r a   u = 0   x = - 1

Será essa última um pedaço de uma reta paralela a x .

Logo, desenhando todas essas três curvas no plano x y , obteremos a nossa região D :)

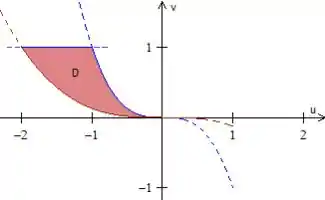
Onde a curva vermelhinha representa y = - x 3 3 e a azul, uma declividade menor, portanto y = - x 3 .

Passo 3

Letra b) Nossa mudança de variáveis foi x = u - v e y = v 3 , logo o jacobiano nas variáveis ( u ,   v ) será

J u , v = ∂ x ∂ u ( u , v ) ∂ x ∂ v ( u , v ) ∂ y ∂ u ( u , v ) ∂ x ∂ v ( u , v )

Calculando essas derivadas parciais aí das funções acima vamos obter

J u , v = 1 - 1 0 3 v 2

Agora resolvendo esse determinante aí, vamos obter

J u , v = 1 - 1 0 3 v 2 = 3 v 2 - 0 = 3 v 2

Passo 4

Letra c) para resolver essa integral aí, a gente pode notar que descrever a região D não é nada harmonioso, principalmente calcular uma integral em cima dela! Qual é a ideia?! É justamente utilizar a região B e suas coordenadas. Assim, teremos a seguinte mudança

x = u - v

y = v 3

J = 3 v 2

Logo, a gente pode fazer

∬ D f x , y d x d y = ∬ B f x ( u ,   v ) , y ( u , v ) ∙ J   d u d v

Lembre-se que quando vamos fazer uma mudança de coordenadas, devemos trocar as coordenadas da função e multiplicar pelo jacobiano e é exatamente isso que queremos com f x ( u ,   v ) , y ( u , v ) ∙ J

Passo 5

A função de x e y é

f x ,   y = 3 π 2 4 x + y 3 2 ∙ sin ⁡ π 2 y

Trocando as variáveis, teremos

f x u ,   v ,   y u ,   v = 3 π 2 4 u - v + v 3 3 2 ∙ sin ⁡ π 2 v 3

Raiz cúbica de v 3 ... morre! Ah! Vou chamar essa função aí apenas de f ( u ,   v ) , beleza?

f u , v = 3 π 2 4 u - v + v 2 ∙ sin ⁡ π 2 v 3 ⇒

f u , v = 3 π 2 u 2 4 ∙ sin ⁡ π 2 v 3

Multiplicando agora pelo jacobiano

f u , v ∙ J = 3 π 2 u 4 ∙ sin ⁡ π 2 v 3 ∙ 3 v 2 =

9 π 2 u 2 4 ∙ sin ⁡ π 2 v 3 ∙ v 2

Passo 6

Vamos agora descrever a região B como do Tipo 1 , beleza? Então vamos olhar mais uma vez para a região B

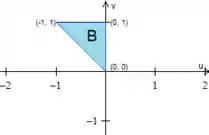
Assim, a gente tem

  • u variando em um intervalo numérico bem definido: - 1 ≤ u ≤ 0
  • v variando da reta inclinada em azul de equação v = - u até v = 1 , ou seja:

- u ≤ v ≤ 1

Passo 7

Prontinho! Nós agora estamos preparados para atacar a integral, bora?

∬ B f x ( u ,   v ) , y ( u , v ) ∙ J   d u d v = ∫ - 1 0 ∫ - u 1 9 π 2 u 2 4 ∙ sin ⁡ π 2 v 3 ∙ v 2 d v d u

Calculando a integral de dentro primeiro com respeito a v utilizando uma substituição do tipo

π 2 v 3 = θ → d θ = 3 π 2 v 2 d v

Não podemos esquecer de mudar os limites de integração

v = - u → θ = - π 2 u 3

v = 1 → θ = π 2

Note que a gente pode dar uma arrumada nessa integral de uma certa forma que possamos ganhar esse d a

∫ - 1 0 ∫ - u 1 9 π 2 u 2 4 ∙ sin ⁡ π 2 v 3 ∙ v 2 d v d u = ∫ - 1 0 ∫ - u 1 3 π u 2 2 ∙ sin ⁡ π 2 v 3 ∙ ( 3 π 2 v 2 d v )   d u ⇒

∫ - 1 0 ∫ - u 1 3 π u 2 2 ∙ sin ⁡ θ ∙ d θ   d u

Calculando agora essa integral em relação a θ e já substituindo os limites de integração...

∫ - 1 0   3 π u 2 2 ( - cos ⁡ θ )   1 - π 2 u 3 π 2 d u ⇒  

∫ - 1 0   3 π u 2 2 - cos ⁡ π 2 + cos ⁡ - π 2 u 3 d u = ∫ - 1 0   3 π u 2 2 cos ⁡ - π 2 u 3 d u ⇒

Lembrando que cos ⁡ - π 2 u 3 = cos ⁡ π 2 u 3

∫ - 1 0   3 π u 2 2 cos ⁡ π 2 u 3 d u

Agora fazendo uma outra substituição muuuuuito semelhante

π 2 u 3 = a → d a = 3 π 2 u 2 d u

E encontrando os limites da nova substituição

u = - 1 → a = - π 2  

u = 0 → a = 0

Teremos

∫ - 1 0   3 π u 2 2 cos ⁡ π 2 u 3 d u = ∫ - π 2 0 cos ⁡ a 3 π u 2 2 d u =

∫ - π 2 0 cos ⁡ a d a

Calculando por fim essa integral e substituindo os limites de integração

∫ - π 2 0 cos ⁡ a d a = ( sin ⁡ a ) - π 2 0 = sin ⁡ 0 - sin ⁡ - π 2 =

1

Resposta

Letra a)

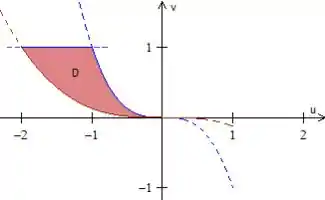
Letra b)

J u , v = 3 v 2

Letra c)

∬ D f x , y d x d y = 1

Exercícios de Livros Relacionados

Determine o jacobiano da transformação.x = v + w^2 , y = w + u^2 , z = u + v^2
Calcule a integral, efetuando uma mudança de variáveis apropriada. ∫ ∫ R x - 2 y 3 x - yd A , onde R é o paralelogramo delimitado pelas retas x - 2 y = 0, x - 2 y = 4, 3 x - y = 1, 3 x - y = 8
Utilize a transformação dada para calcular a integral. ∬ R 4 x + 8 y d A , onde R é o paralelogramo com vértices - 1,3 , 1 , - 3 , 3 , - 1 e 1,5 ; x = 1 4 u + v , y = 1 4 v - 3 u
Calcule ∫ ∫ D y + 2 x y - 2 x - 1 d x d y , onde D é a região do plano x y limitada por y - 2 x = 2 , y + 2 x = 2 , y - 2 x = 1 e y + 2 x = 1 .
Calcule ∫ ∫ D xd x d y , onde D é a região do plano x y limitada pelas parabolas x = y 2 - 1 , x = 1 - y 2 e x = 4 - y 2 4 .