Considere a integral

onde é a região limitada pelas , , e .

Desenhe a região de integração. Justifique...

Calcule a integral . Justifique...

Bom galera, nossa preocupação agora é desenhar a região . Vimos no passo anterior as curvas que delimitam essa superfície, mas vocês lembram como é o gráfico dessas curvas?

Vamos dar uma revisada com calma! Basicamente, temos dois polinômios cúbicos:

O gráfico de polinômios de grau , tem essa cara daqui:

Podendo ter uma ou três raízes reais (dependendo do polinômio).

No caso das nossas curvas, especificamente, temos que:

Portanto, é a única raiz real dessa primeira curva.

Portanto, é a única raiz real dessa segunda curva.

Além disso, será que essas duas curvas se intersectam em algum ponto?

Para verificar isso, basta igualarmos as duas equações:

O que é um absurdo matemático! Logo, as curvas não se intersectam. Com essas informações, podemos desenhar essas duas curvas juntas em um mesmo gráfico:

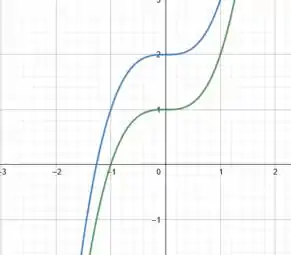
Massa!

Vamos pensar agora nas nossas retas:

Essas retas são bem simples, pois elas passam pela origem, já que pertence a elas.

Além disso, a origem é o único ponto de intersecção delas duas:

Massa! Então, também podemos plotá-las no gráfico:

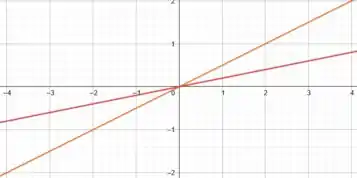
Perfeito! Agora precisamos juntar todas essas curvas em um único gráfico para encontrar a região que é delimitada por elas.

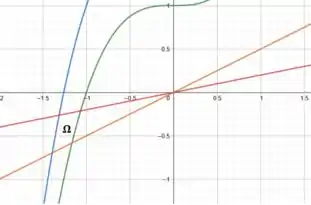
Prontinho! Encontramos a nossa região ali no canto inferior.

Uma dúvida que a gente pode ter quando estamos desenhando essas curvas sem auxílio do computador, é se as retas vão intersectar as curvas cúbicas nos valores positivos de ou nos valores negativos.

Para saber isso, devemos buscar calcular essas intersecções. Ou seja, precisamos igualar as equações. Por exemplo:

O problema é que essa equação é cúbica, e não tem uma raiz fácil de encontrarmos por inspeção (o mesmo ocorre na intersecção das outras curvas).

Nesse caso, como aqui precisamos apenas esboçar a região, podemos fazer uma análise numérica da expressão pra tentar descobrir. Pensa comigo:

Se então vai ser sempre maior do que . Assim, se nunca teremos a igualdade da curva e da reta.

Agora, se , até vai ser menor do que . Mas, a expressão do lado esquerdo é , que nesse intervalo é sempre maior do que . Já do lado direito temos , que nesse intervalo é sempre menor do que .

Ou seja, se as curvas e retas não se intersectam. Assim, podemos esboçar sem dor na consciência a nossa região aparecendo para .

Pegou bem a ideia?

É isso! A primeira parte já foi 😊

Agora precisamos calcular essa integral de superfície!

Precisamos transformá-la em uma integral dupla normal. Podemos fazer isso através do método direto (parametrizando a superfície, calculando o vetor normal e etc), ou realizando uma mudança de variáveis.

Qual vocês acham que se encaixaria melhor nesse caso?

Hahaha! Precisamos pensar na dificuldade que essa integral está passando pra gente. Uma parte muito delicada é que não conseguimos identificar exatamente quais são os pontos de intersecção entre as curvas que delimitam a região .

Assim, se optarmos pelo método direto iremos esbarrar nos limites de integração, além de que seria muito difícil parametrizar essa superfície (já que ela não se encaixa em nenhum dos casos clássicos que conhecemos).

Já se utilizarmos a mudança de variáveis, podemos buscar novas variáveis que sejam mais tranquilas de encontrarmos o intervalo de variação. Isso já resolve o problema dos limites de integração! Vamo nessa então?!

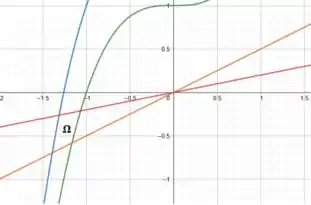
Essa é a nossa região . Lateralmente ela é delimitada pelas curvas:

Podemos então tentar definir uma variável que represente essa limitação lateral. Uma dica aqui é já pensarmos nos intervalos de integração! Então, se definirmos:

teremos que na limitação lateral esquerda de é justamente a curva . Assim, vale:

Já na limitação à direita, teremos:

Portanto, fazer essa mudança de variável é bem proveitoso pois temos:

Entendeu bem essa ideia?

Vamos pensar agora nas limitações inferior e superior. Se definirmos:

Em ambas as retas conseguimos isolar essa razão e encontrar um número para limitar o intervalo de variação de :

Analogamente:

Portanto, temos:

Muito bom! Vencemos uma das principais dificuldades dessa integral, que era determinar os limites de integração 😊

Lembra que, sempre que fazemos uma mudança de variáveis em integral dupla precisamos calcular um novo terminho... que éeeee?

O Jacobiano!! Ele é dado por:

Resolvendo esse determinante, temos:

Vamos então buscar calcular esses dois termos.

Temos que:

Derivando parcialmente em relação a , vem:

Substituindo em ficamos com:

Colocando em evidência:

Derivando agora parcialmente em relação a , temos:

Usando a regra do produto no lado esquerdo:

Logo:

Essa expressão é justamente o que apareceu em . Então, substituído, temos:

Massa! Nosso problema se resume a calcular . Usando que:

E, derivando essa equação parcialmente em relação a , e usando a regra da cadeia em , temos:

Além disso, da equação que desenvolvemos, temos que:

Substituindo esse resultado:

Usando que e isolando , finalmente chegamos que:

Portanto, voltando ao nossos Jacobiano, temos:

E, como as intersecções das curvas ocorrem em (caso contrário , enquanto pra , por exemplo, e a intersecção não ocorreria), temos também que o módulo do Jacobiano vale:

Prontinho!!

É galera, entendo vocês! Essa questão tá puxada mesmo. Mas, já chegamos até aqui, não podemos desistir de aprender ela. Está mais perto do fim do que do começo hahaha! Vamo lá!

Até agora já fizemos nossa mudança de variáveis:

Também já calculamos o nosso Jacobiano.

Temos também que:

Vamos então substituir tudo isso na nossa integral e ver o que está faltando:

Olha que lindo gente! Foi por isso que não tentamos calcular antes , pois quando substituímos na integral muitos termos se cancelam. Assim, ficamos com:

Só que nossas variáveis de integração são e , então vamos eliminar e da jogada lembrando que:

Tranquilo? Daí:

Logo:

Assim:

Finalmenteeee:

Portanto, essa integral de superfície cabulosíssima, vale:

Ufaaaaaaa!!! Quem tá morto de cansado levanta a mãooooo!!

Mas terminamos pessoal! VENCEMOSSSS!! Agora tira uma pausa pra beber uma água, tomar um café, e já vem ver a próxima questão com a gente!

Espero que vocês tenham curtido, até a próxima galera 😊