Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança Qualquer de Variáveis

Ver Teoria
Exercício 1312345678910111214151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283

Enunciado

  1. Calcule as seguintes integrais:

∬ D   x - y x + y 2 d x d y

D é a região triangular de vértices 0 ,   0 ,   1 ,   0   e   0 ,   1 .

Passo 1

Bem, essa integral parece esquisita e difícil de calcular, né?

Então vamos tentar fazer uma mudança de variável pra ver se simplifica as coisas. Seria muito bom se uma das variáveis fosse

u = x + y

e a outra

v = x - y

Mas vamos entender a região, primeiro, pra ver se dá pra fazer assim mesmo.

Passo 2

Podemos desenhar esse triângulo aí simplesmente obedecendo ao problema e colocando esses pontos no plano cartesiano

Em seguida ligando os pontos por retas...

Pegou? Viu quem é a região?

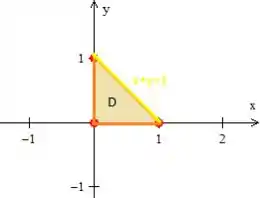
Repare que essa hipotenusa do triangulo está em cima da reta x + y = 1 , afinal de contas, quando x = 0 , y = 1 e vice versa.

Então de fato, realizar essa mudança simplifica muito as contas.

Passo 3

Você não pode se esquecer de que toda mudança exige que determinemos os limites dos novos termos, no caso é o u e o v .

Para o limite de u , é bem fácil, afinal sabemos que u = x + y e na região o valor máximo de x + y = 1 . Logo

0 ≤ u ≤ V a l o r   m á x i m o

0 ≤ u ≤ 1

Quanto ao v , bem, vamos usar as informações das retas que não usamos... No caso é a reta x = 0 e y = 0 :

Montando um sistema com as mudanças

x - y = v x + y = u

substituindo o valor de x = 0 nesse sisteminha

v = - u

e substituindo o valor de y = 0 ...

v = u

onde tiramos que

- u ≤ v ≤ u

Passo 4

Não podemos nos esquecer de modo algum que esse tipo de mudança exige que encontremos o J a c o b i a n o   J .

Porém, o jacobiano a gente calcula a partir de J a c o b i a n o   I n v e r s o   J * , já que temos as variáveis u e v isoladas, ao invés de x e y :

J * = ∂ ( u , v ) ∂ ( x , y )     = ∂ u ∂ x ∂ u ∂ y ∂ v ∂ x ∂ v ∂ y

como

u = x + y

v = x - y

Basta que calculemos essas derivadas em seguida resolver esse determinante, saca?

∂ u ∂ x = 1           ∂ u ∂ y = 1

∂ v ∂ x = 1         ∂ v ∂ y = - 1

J * = 1 1 1 - 1 = - 2

Então, temos:

J = 1 J *     →     J = 1 2

Passo 5

Finalmente, podemos retornar a integral substituindo tuuudo:

∬ D   x - y x + y 2 d x d y =

∫ 0 1 ∫ - u u v u 2 ∙ J   d v d u =

1 2 ∫ 0 1 ∫ - u u v 2 u 2 d v d u

Agora é só calcular essa integral como manda os bons costumes, ou seja, primeiro a de dentro em termos de v (logo, considerando 1 u 2 como uma constante)...

1 2 ∫ 0 1 ∫ - u u v 2 u 2 d v d u = 1 2 ∫ 0 1 1 u 2 ∫ - u u v 2 d v d u =

Integrando e substituindo...

1 2 ∫ 0 1 1 u 2 v 3 3 - u u d u =

1 2 ∫ 0 1 1 u 2 u 3 3 - - u 3 3 d u =

1 2 ∫ 0 1 1 u 2 u 3 3 + u 3 3 d u =

1 2 ∫ 0 1 1 u 2 2 u 3 3 d u = 1 3 ∫ 0 1 u   d u = 1 3 u 2 2 0 1

= 1 6

Resposta

Exercícios de Livros Relacionados

Determine o jacobiano da transformação.x = v + w^2 , y = w + u^2 , z = u + v^2
Calcule a integral, efetuando uma mudança de variáveis apropriada. ∫ ∫ R x - 2 y 3 x - yd A , onde R é o paralelogramo delimitado pelas retas x - 2 y = 0, x - 2 y = 4, 3 x - y = 1, 3 x - y = 8
Utilize a transformação dada para calcular a integral. ∬ R 4 x + 8 y d A , onde R é o paralelogramo com vértices - 1,3 , 1 , - 3 , 3 , - 1 e 1,5 ; x = 1 4 u + v , y = 1 4 v - 3 u
Calcule ∫ ∫ D y + 2 x y - 2 x - 1 d x d y , onde D é a região do plano x y limitada por y - 2 x = 2 , y + 2 x = 2 , y - 2 x = 1 e y + 2 x = 1 .
Calcule ∫ ∫ D xd x d y , onde D é a região do plano x y limitada pelas parabolas x = y 2 - 1 , x = 1 - y 2 e x = 4 - y 2 4 .