Mudança de variáveis
Considere a integral
Onde é o paralelogramo delimitado pelas retas , , e .
- Escolha uma mudança de variáveis apropriada (note que . Calcule a derivada .
- Esboce cuidadosamente as regiões de integração , onde .
- Calcule a integral usando a fórmula de mudança de variáveis.
Passo 1
Letra a)
Bom, reparou que e aparecem vezes nessa questão, né? Então é essa mudança que vamos fazer:
Beleza?
Passo 2
Bom, se vamos fazer um mudança de variáveis, precisamos calcular o Jabobiano disso aí. Temos a transformação:
O que nos dá
Como
Passo 3
Letra b)
Agora temos que descobrir nossa região de integração no plano . Sabemos que é o paralelogramo delimitado pelas retas , , e . Fazendo a mudança de variáveis nessas equações, temos:
Graficamente
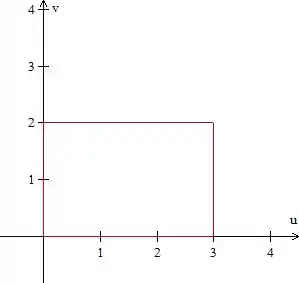
A região de integração é o interior desse retângulo.
Passo 4
Letra c)
Show, agora vamos escrever matematicamente essa região. Podemos ver pela figura que:
Passo 5
Agora vamos fazer a mudança na nossa integral.
Não se esqueça do Jacobiano!
E resolver isso aí:
Resposta
Exercícios de Livros Relacionados
Determine o jacobiano da transformação.x = v + w^2 , y = w + u^2 , z = u + v^2
Calcule a integral, efetuando uma mudança de variáveis apropriada. ∫ ∫ R x - 2 y 3 x - yd A , onde R é o paralelogramo delimitado pelas retas x - 2 y = 0, x - 2 y = 4, 3 x - y = 1, 3 x - y = 8
Utilize a transformação dada para calcular a integral. ∬ R 4 x + 8 y d A , onde R é o paralelogramo com vértices - 1,3 , 1 , - 3 , 3 , - 1 e 1,5 ; x = 1 4 u + v , y = 1 4 v - 3 u
Calcule ∫ ∫ D y + 2 x y - 2 x - 1 d x d y , onde D é a região do plano x y limitada por y - 2 x = 2 , y + 2 x = 2 , y - 2 x = 1 e y + 2 x = 1 .
Calcule ∫ ∫ D xd x d y , onde D é a região do plano x y limitada pelas parabolas x = y 2 - 1 , x = 1 - y 2 e x = 4 - y 2 4 .