USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 1 - 2022.1, Questão 15a
Calcule usando mudança de coordenadas:
a) , onde é o paralelogramo de vértice , , e .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular uma integral meio estranha em um domínio no formato de paralelogramo. Isso é a dica para a gente usar uma mudança de variáveis linear!
Como assim? Mudança de variáveis linear é quando a gente aplica uma mudança com expressões assim no nosso domínio:
Onde são constantes. A ideia é que essa mudança vai deixar nosso integrando bonito e vai transformar nosso domínio de paralelogramo para um retângulo! Sonho, né? Vamos usar isso então! Mas que expressões podemos testar para e ? Vamos ver isso pelo integrando:
De cara, a gente já acha uma expressão linear que podemos usar:
Para achar a outra, a gente pode usar produtos notáveis para reescrever o integrando:
Daí a gente acha a outra expressão:
Agora é ver se ela funciona bem no domínio. Vamos lá!
Passo 2
Para a mudança
ser super útil para a gente, ela precisa transformar nosso domínio em um retângulo. E como a gente vê se isso acontece?
Vamos passar os vértices do nosso paralelogramo por essa mudança de variáveis, e ver se os vértices novos formam um retângulo no plano . Assim:
-
Daí temos o ponto
-
Daí temos o ponto
-
Daí temos o ponto
-
Daí temos o ponto
Aí desenhando no plano , o paralelogramo de vértices e :
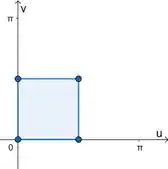
Temos realmente um retângulo! Aí isso diz que essa mudança é maravilhosa para a gente. Vamos usar ela mesmo! E para descrever esse retângulo como extremos de integração, a gente pode dizer que:
Passo 3
Para montar o integrando a gente precisa do jacobiano da nossa mudança.
Maas, como a gente tem e em função de , vamos calcular o inverso disso:
Bora lá:
Aí a gente inverte
E tira o módulo:
Passo 4
A integral que a gente tinha era:
Mas a gente saiu de e foi para . Então, precisamos fazer algumas modificações. Primeiro, vamos colocar nossos novos extremos de integração e multiplicar esse integrando por :
A gente precisa agora colocar esse integrando em função de e . Lembrando que a gente escreveu ele assim:
Já que :
Pronto! Agora ele está todo em .
Passo 5
Só falta calcular a integral:
Vamos usar a substituição simples , nessa integral de dentro
Aí a integral fica
Calculando agora em relação a e aplicando os intervalos:
Valeu, galera! Até a próxima! 😉